Fundamentals of Fluid Flow in Porous Media
Chapter 4
Immiscible Displacement
Buckley-Leverett Theory
One of the simplest and most widely used methods of estimating the advance of a fluid displacement front in an immiscible displacement process is the Buckley-Leverett method In many rocks there is a transition zone between the water and the Oil zones. In the true water zone, the water saturation is essentially 100. In the oil zone, there is usually present connate water, which is essentially immobile. Only water will be produced from a well completed in the true water zone, and only oil will be produced from the true oil zone. In the transition zone both oil and water will be produced, and at each point the fraction of the flowrate that is water will depend on the oil and water saturations at that point. Frontal advance theory is an application of the law of conservation of mass. Flow through a small volume element () with length ∆x and cross-sectional area “A” can be expressed in terms of total flow rate qt as: Where q denotes volumetric flow rate at reservoir conditions and the sub-scripts {o,w,t} refer to oil, water, and total rate, respectively and ƒw and ƒo are fractional flow to water and oil (or water cut and oil cut) respectively: ko / kw is a function of saturation. So for constant viscosity ƒw is just a function of saturation. Figure 4‑1 is a plot of the relative permeability ratio, ko / kw, versus water saturation. Because of the wide range of ko / kw values, the relative permeability ratio is usually plotted on the log scale of semi-log paper. Like many relative permeability ratio curves, the central or main portion of the curve is quite linear. As a straight line on semi-log paper, the relative permeability ratio may be expresses as a function of the water saturation by: The constants “a” and “b” may be determined from the graph, such as Figure 4‑1, or determined from simultaneous equations from known data of saturation and relative permeability. Substituting eq. (4‑6) into eq. (4‑5) will end with: If the water fractional flow is plotted versus water saturation, an S-shaped curve will result that is named fractional flow curve. Assume that the total flow rate is the same at all the medium cross section. Neglect capillary and gravitational forces that may be acting. Let the oil be displaced by water from left to right. The rate the water enters to the medium element from left hand side (LHS) is: The rate of water leaving element from the right hand side (RHS) is: The change in water flow rate across the element is found by performing a mass balance. The movement of mass for an immiscible, incompressible system gives: Change in Water Flowrate = water entering – water leaving This is equal to the change in element water content per unit time. Let Sw is the water saturation of the element at time t. Then if oil is being displaced from the element, at time ( t + Δt ) the water saturation will be ( Sw + ΔSw ). So water accumulation in the element per unit time is: Where, φ is porosity. Equating equations (4‑10) and (4‑11) results: In the limit as ∆t → 0 and ∆x → 0 (for the water phase): The subscript x on the derivative indicates that this derivative is different for each element. It is not possible to solve for the general distribution of water saturation Sw( x,t ) in most realistic cases because of the nonlinearity of the problem. For example, water fractional flow is usually a nonlinear function of water saturation. It is therefore necessary to consider a simplified approach to solving Eq. ((4‑13)). For a given rock, the fraction of flow for water ƒw is a function only of the water saturation Sw, as indicated by Eq. (4‑13), assuming constant oil and water viscosities. The water saturation however is a function of both time and position, which may be express as ƒw = F( Sw ) and Sw = G( t,x ). Then: Now, there is interest in determining the rate of advance of a constant saturation plane, or front ( ∂x / ∂t )Sw , where Sw is constant and dSw = 0. So from eq. (4‑14): Substituting eqs (4‑13) and 4‑15) into eq. (4‑16) gives the Buckley-Leverett frontal advance equation: The derivative This means that the distance a plane of constant saturation, Sw, advances is proportional to time and to the value of the derivative ( Where, xSwis the distance traveled by a particular Sw contour Qinj is the cumulative water injection at reservoir conditions. In field units: Example 4-1 Assume a cubical reservoir under active water drive with oil production of 900bbl/day. The flow could be approximated as a linear flow. The cross sectional area is the product of the width, 1320 ft, and the true formation thickness, 20 ft, so that for a porosity of 0.25, eq. (4‑19) becomes: Consider that because we assume the fluids are completely incompressible, so the oil production rate is equal to the total flowrate in the different cross sections of the reservoir. If we let x=0 at the first point of the transition zone, then the distances the various constant water saturation planes will travel in, say, 60, 120, and 240 days are given by: The value of the derivative The derivative Figure 4‑5 shows the water fractional flow curve and also the derivative A plot of Sw versus distance using Eq. (4‑20) and typical fractional flow curves leads to the physically impossible situation of multiple values of Sw at a given location. For example Figure 4‑6 shows water saturation distribution according to eqs (4‑20) and (4‑21). For example, at 50% water saturation, the value of the derivative is 2.87; so by eq. (4‑20), at 60 days the 50% water saturation plane will advance a distance of: This distance is plotted as shown in Figure 4‑6 along with the other distances that have been calculated using eqs (4‑20) and (4‑21) for other time values and other water saturations. These curves are characteristically double-valued or triple valued. For example, Figure 4‑6 indicates that the water saturation after 240 days at 400 ft is 20, 39, and 69%. The saturation can be only one value at any place and time. What actually occurs is that the intermediate values of the water saturation have the maximum velocity (Figure 4‑5 and eq. (4‑17)), will initially tend to overtake the lower saturations resulting in the formation of a saturation discontinuity or shock front. Because of this discontinuity the mathematical approach of Buckley-Leverett, which assumes that Sw is continuous and differentiable, will be inappropriate to describe the situation at the front itself. The difficulty is resolved by dropping perpendiculars at point Xƒ (as flood front position) so that the areas to the right (A) equal the areas to the left (B), as shown in Figure 4‑6. In other words a discontinuity in Sw at a flood front location Xƒ is needed to make the water saturation distribution single valued and to provide a material balance for displacing fluid. A more elegant method of achieving the same result was presented by Welge in 1952. This consists of integrating the saturation distribution over the distance from the injection point to the front, thus obtaining the average water saturation behind the front Sw, as shown in Figure 4‑7[3]. The situation depicted is at a fixed time, before water breakthrough, corresponding to an amount of water injection. At this time the maximum water saturation, Sw = 1 – Sor, has moved a distance X1, its velocity being proportional to the slope of the fractional flow curve evaluated for the maximum saturation which, as shown in Figure 4‑5, is small but finite. The flood front saturation Swƒ is located at position x2 measured from the injection point. Applying the simple material balance: So: Where, Qinj is cumulative water injection. Using eq. (4‑18): At breakthrough time: Where, tbt = Breakthrough time, qt = Total injection rate, L = Medium length From eq. (4‑24): Where PVI is the pore volume injected. So: The average water saturation in the reservoir at the time of breakthrough is given by material balance as: From eqs (4-26) and (4-27): Therefore: To satisfy eq. (4‑29) the tangent to the fractional flow curve, from the point Sw = Swc, where ƒw = 0, must have a point of tangency with co-ordinates Sw = Swƒ; ƒw = ƒwƒ, and extrapolated tangent must intercept the line ƒw = 1 at the point (Sw = Swbt ; ƒw = 1). See Figure 4‑8. The use of either of these equations ignores the effect of the capillary pressure gradient, ∂Pc / ∂x. This simple graphical technique of Welge has much wider application in the field of oil recovery calculations. As eq. (4‑19) shows the velocity of every saturation front is constant, the graph of saturation location vs. time is set of straight lines starting from the origin. This graph is often plotted in dimensionless form. The equation can be made dimensionless by defining: Where xD = Normalized distance tD = Pore volumes injected Eq. (4‑19) becomes: Figure 4‑9 is a graph of dimensionless distance vs. dimensionless time for the movement of water saturation predicted by the frontal advance equation. Saturation Siw < Sw < Swƒ travel at the same velocity are located on the flood-front path. The region ahead of flood front has a uniform saturation. Saturations greater than Swƒ travel at progressively slower velocities as indicated by the decreasing slopes in Figure 4‑9. Saturation profiles or saturation histories can be constructed by making cross sections through the time/distance graph. A saturation profile is a graph of the locations of all saturations along a cross section of fixed time, as illustrated by the continuous line at tD = 0.28 in Figure 4‑9. Figure 4‑10 displays the saturation profile at tD = 0.28 that was obtained from Figure 4‑9. The saturation history is the graph of saturation vs. time at a particular value of xD. A plot of water saturation vs. tD for xD = 1, shown in Figure 4‑11, illustrates the arrival of water saturations at the end of the linear system. Figure 4‑12 represents the initial water and oil distributions in the reservoir unit and also the saturation distributions after 240 days, provided the flood front has not reached the produced face of the cubic reservoir. The area to the right of the flood front in Figure 4‑12 is commonly called the oil bank and the area to the left is sometimes called the flooded or drag zone. The area above the 240-day curve and below the 90% water saturation curve represents oil that may yet be recovered, or dragged out of the high-water saturation portion of the reservoir by flowing large volumes of water through it. The area above the 90% water saturation represents unrecoverable oil since the critical oil saturation is 10%. This presentation of the displacement mechanism has assumed that capillary force is negligible. Figure 4‑12 also indicates that a well in this reservoir will produce water-free oil until the flood front approaches the well. Thereafter, in a relatively short period, the water cut will rise sharply and be followed by a relatively long period of production at high, and increasingly higher, water cuts. For example, just behind the flood front at 240 days, the water saturation rises from 20% to about 60%-that is, the water cut rises from zero to 66% (see Figure 4‑5). When a producing formation consists of two or more rather definite strata, or stringers, of different permeabilities, the rates of advance in the separate strata will be proportional to their permeabilities, and the overall effect will be a combination of several separate displacements, such as described for a single homogeneous stratum. [1] “Principle of applied reservoir simulation”, John R. Fanchi [2] “Applied Petroleum Reservoir /engineering”, B.C. Craft, M. Hawkins, 1991 [3] “Fundamentals of Reservoir Engineering”, L.P. Lake, 1978. If you have any questions at all, please feel free to ask PERM! We are here to help the community.

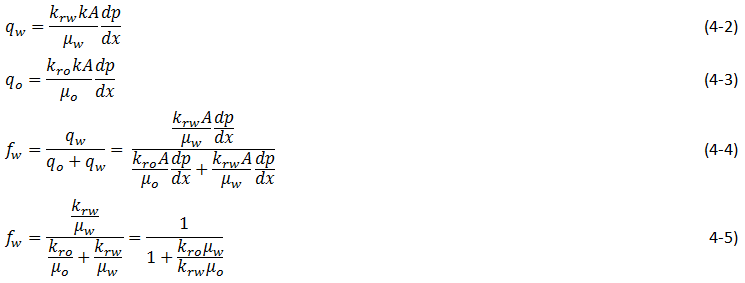

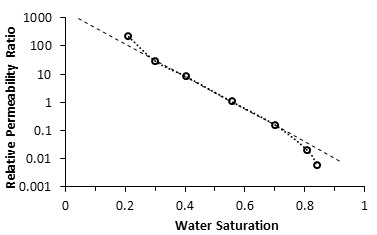
Figure 4-1: Semilog Plot of Relative Permeability Ratio versus Saturation

Figure 4-2: Fractional Flow Curve
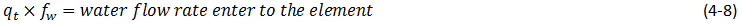
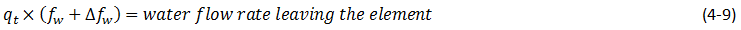
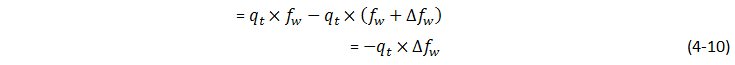
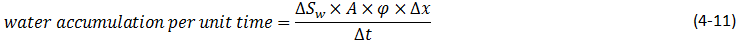


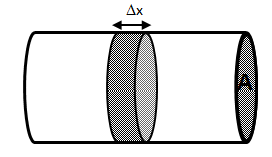
Figure 4-3: Horizontal Bed Containing Oil and Water



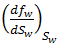 is the slope of the fractional flow curve and derivative
is the slope of the fractional flow curve and derivative 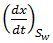 is the velocity of the moving plane with water saturation Sw. Because the porosity, area, and flowrate are constant and because for any value of Sw, the derivative
is the velocity of the moving plane with water saturation Sw. Because the porosity, area, and flowrate are constant and because for any value of Sw, the derivative 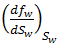 is a constant, then the rate dx / dt is constant.
is a constant, then the rate dx / dt is constant.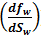 ) at that saturation, or:
) at that saturation, or:

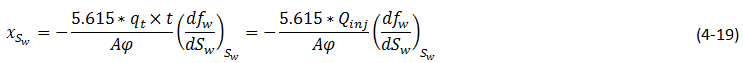
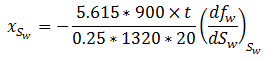
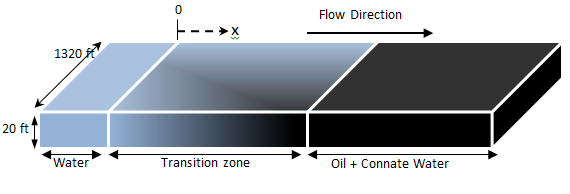
Figure 4-4: Cubic Reservoir Under Active Water Drive

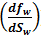 may be obtained for any value of water saturation, Sw, by plotting ƒw from eq. (4‑7) versus Sw and graphically taking the slopes at various values of Sw. Assume you find a=1222 and b=12 from Figure 4‑1 (intercept = 1222 = ‘a’ and slope of the straight line = 13 = ‘b’) for eq. (4‑7). For example at Sw = 0.4, ƒw = 0.129. The slope taken graphically at Sw = 0.4 and ƒw = 0.267 is 1.66.
may be obtained for any value of water saturation, Sw, by plotting ƒw from eq. (4‑7) versus Sw and graphically taking the slopes at various values of Sw. Assume you find a=1222 and b=12 from Figure 4‑1 (intercept = 1222 = ‘a’ and slope of the straight line = 13 = ‘b’) for eq. (4‑7). For example at Sw = 0.4, ƒw = 0.129. The slope taken graphically at Sw = 0.4 and ƒw = 0.267 is 1.66.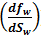 may also be obtained mathematically using eq.(4‑7):
may also be obtained mathematically using eq.(4‑7):

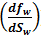 plotted against water saturation from eq. (4‑21). Since Eq. (4‑7) does not hold for the very high and for the quite low water saturation ranges (see Figure 4‑1), some error is introduced below 30% and above 80% water saturation. Since these are in the regions of the lower values of the derivatives, the overall effect on the calculation is small.
plotted against water saturation from eq. (4‑21). Since Eq. (4‑7) does not hold for the very high and for the quite low water saturation ranges (see Figure 4‑1), some error is introduced below 30% and above 80% water saturation. Since these are in the regions of the lower values of the derivatives, the overall effect on the calculation is small.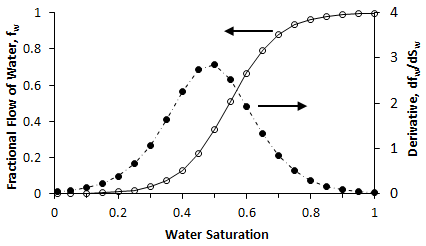
Figure 4-5: Water Fractional Flow and its Derivative
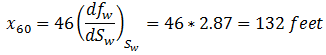
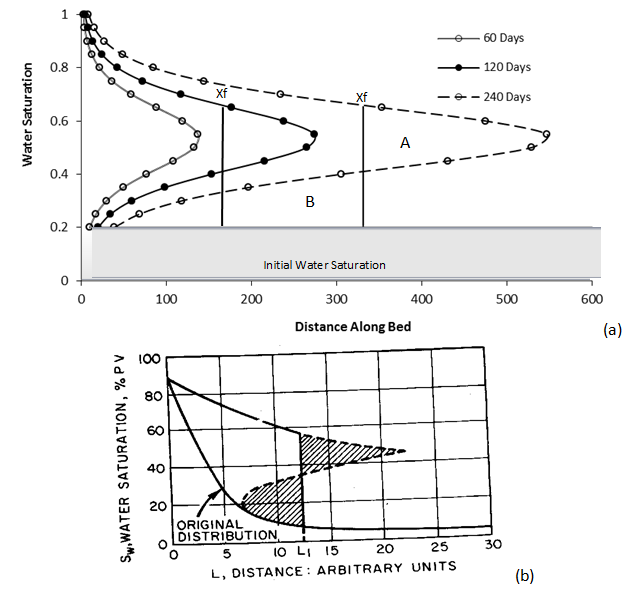
Figure 4-6: (a) Fluid Distribution at 60, 120, 240 days (b) Triple-Valued Saturation Distribution (After Buckley and Leverett, 1942)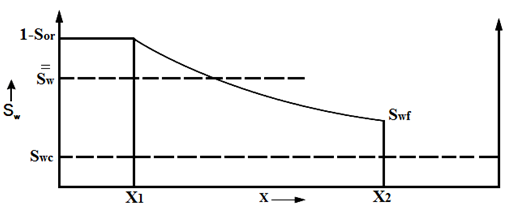
Figure 4-7: Water Saturation Distribution as a Function of Distance, Prior to Breakthrough









i.e. the slope of the fractional flow curve at conditions of the front is given by eq. 4‑29).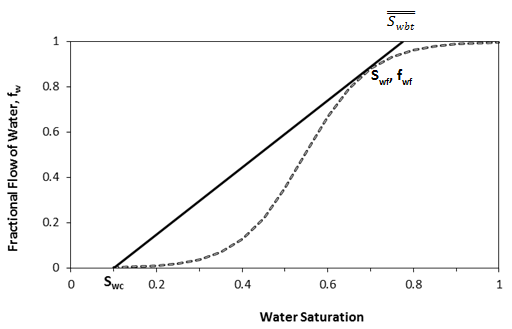
Figure 4-8: Tangent to the Fractional Flow Curve from Sw = Swc


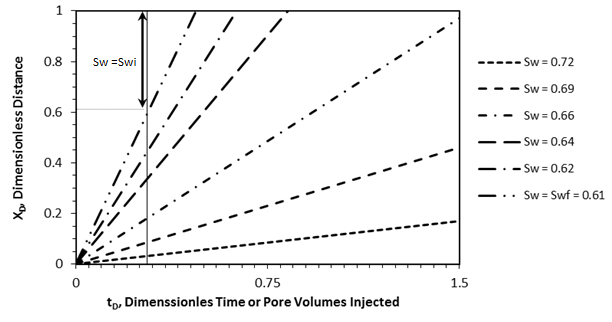
Figure 4-9: xo vs. tD for a Linear Waterflooding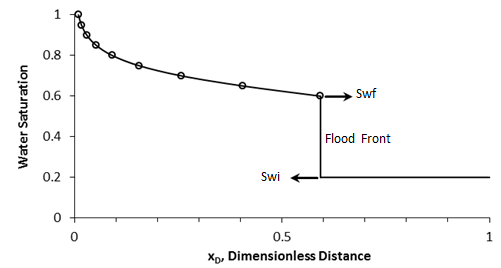
Figure 4-10: Saturation Profile at tD = 0.28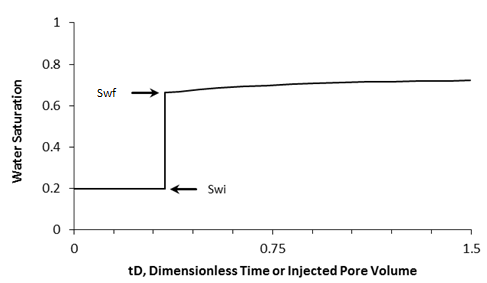
Figure 4-11: Saturation History at xD = 1, Producing Face of the Medium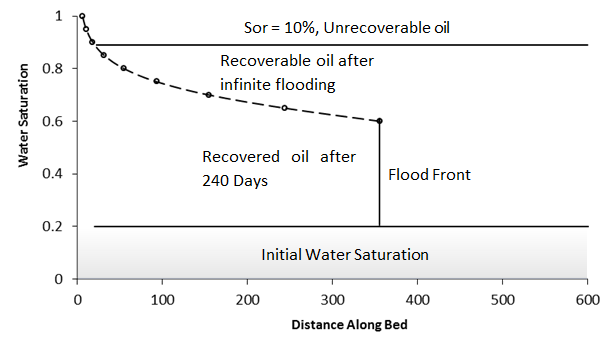
Figure 4-12: Saturation Distribution After 240 DaysReferences
Questions?
