Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Permeability:

Permeability of Combination Layers

The foregoing flow equations were all derived on the basis one continuous value of permeability between the inflow and out flow face. It is rare to encounter a homogeneous reservoir in actual practice. Most formations have space variations of permeability. They are more variable than porosity and more difficult to measure. Yet an adequate knowledge of permeability distribution is critical to the prediction of reservoir depletion by any recovery process.

In many cases, the reservoir contains distinct layers, blocks, or concentric rings of varying permeabilities. Also, because smaller-scale heterogeneities always exist, core permeabilities must be averaged to represent the flow characteristics of the entire reservoir or individual reservoir layers (units). The proper way of averaging the permeability data depends on how permeabilities were distributed as the rock was deposited. There are three simple permeability-averaging techniques that are commonly used to determine an appropriate average permeability to represent an equivalent homogeneous system. These are:

• Weighted-average permeability
• Harmonic-average permeability
• Geometric-average permeability

Weighted-Average Permeability:

This averaging method is used to determine the average permeability of layered-parallel beds with different permeabilities. Consider the case where the flow system is comprised of three parallel layers that are separated from one another by thin impermeable barriers, i.e., no cross flow, as shown in Figure 2‑23. All the layers have the same width w with a cross-sectional area of A.

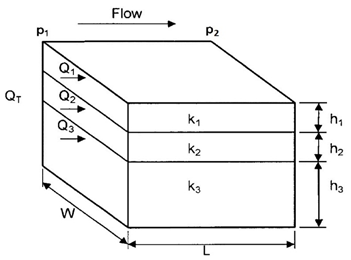
Figure 2-23: Linear Flow through Layered Bed

The flow from each layer can be calculated by applying Darcy’s equation in a linear form as expressed by equation (2‑28), to give:

Layer 1

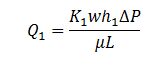
Layer 2

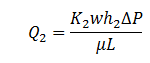
Layer 3

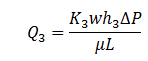
The total flow rate from the entire system is expressed as

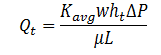
The total flow rate Q_t is equal to the sum of the flow rates through each layer or:

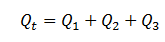
Substitution of value for each term:

General expression for average permeability of a parallel layered formation with n layers is:

The presented general formula for a parallel layered formation which each layer has its own width (‘w’ in Figure 2‑23) is as follows: