Fundamentals of Fluid Flow in Porous Media
Chapter 3
Diffusion Coefficient: Measurement Techniques
Pressure Decay Method
Among indirect methods, the pressure decay method has attracted more attention due to its simplicity in terms of experimental measurements. In this method, gas (as a solvent) and oil are injected into a cell (Figure 3‑6). The cell content is initially at a non-equilibrium state. As the experiment progresses, the gas dissolve into the oil and the pressure inside the cell decreases as a result. By recording the pressure and the level of the liquid in the cell, the amount of gas transferred into the oil can be determined. From this, the diffusion coefficient is calculated. In cases involving complex hydrocarbon mixtures with possible multiphase behaviors, the pressure decay method fails. This method, however, had been discredited by Luo and Gu This method was first applied by Riazi[2] and for dissolution of methane in n-pentane. He took the non-equilibrium gas into contact with n-pentane in a sealed container at a constant temperature. He determined the final state by thermodynamic equilibrium. However, the time which was required to reach the final state was determined from the diffusion process in each phase. He assumed that at the gas-liquid interface, thermodynamic equilibrium exists between the two phases at all times. However the position of the interface as well as the pressure may change with time. The rate of change of pressure and the interface position as a function of time depends on the rate of diffusion in each phase and therefore on the diffusion coefficients. Other researchers have proposed and developed different mathematical solutions by modeling the interface boundary condition differently. Modeling the physics of the interface (when the pressure is declining) often requires complex mathematical solutions, and it is known that more simplified analysis based on assumption of constant equilibrium concentration at the interface introduces significant error in the estimation of the diffusion coefficient. To overcome some of these shortcomings different researcher used different models. Upreti and Mehrotra[3] improved the pressure decay method to find concentration dependent diffusion coefficient. Their experimental apparatus primarily consists of a closed cylindrical pressure vessel used to hold gas over a layer of bitumen. A pump supplied the gas as a solvent at desired pressure into the vessel. The vessel was submerged in a constant temperature water bath, the pressure vs. time data were recorded by a pressure sensor. Using the logged pressure versus time data, the experimental mass of a given gas diffused into the bitumen was determined. The gas diffusivity was then calculated by fitting the calculated mass of the gas diffused into bitumen (given by a mass transfer model) to the experimental mass. The tuning parameter was the diffusion coefficient. Additionally a correlation was provided for the average diffusivity as a function of temperature. [1] Luo, P. and Y. Gu, Fluid Phase Equilibria, 2009 [2] Riazi, M. R., J. Pet. Sci. Eng. 1996 [3] Upreti, S., Lohi, A., Kapadia, R. and El-Haj, R., 2007 If you have any questions at all, please feel free to ask PERM! We are here to help the community.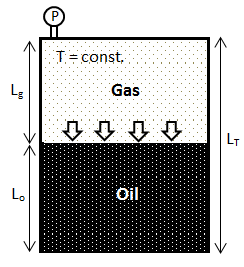
Figure 3-6: Pressure Decay Test CellReferences
Questions?
