Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Formation Resistivity Factor

Porous media consist of mineral, rock fragments and void space. The solids with exception of certain clay minerals (such as shaly sands where clay shales produce electrical conductivity) are nonconductive. Generally the electrical property of a rock depends on void space geometry and the fluids that occupy the void space. The fluid of interest for petroleum engineers are oil, gas and water. Oil and gas are nonconductor and water is conductive when contains dissolved salts.  Water has electrolyte conductivity, because electricity conducted by movement of ions. The resistivity term, as the reciprocal of conductivity, is used to define the ability of a material to conduct current:

Where:

• r = resistance, ohm
• R = resistivity of, ohm-cm
• A = Cross section area, cm²
• L = Length, cm

“Formation Resistivity Factor” is the most fundamental concept in considering electrical properties of rock:

Where:

• R_o = Resistivity of fully water saturated rock
• R_w = Saturating water resistivity

It is only defines for porous matrices of negligible electrical conductivity. It is evident that F is always greater than unity in the absence of electrical conductive layers. The formation resistivity factor measure the influence of pore structure on the resistance of sample. In the absence of a conductive mineral layer the electrical current can flow only through the fluid in the rock interconnected pores. This implies that F is related to the porosity of the rock. The influence of pore structure on the electrical conductivity may be divided into two contributions: the reduction of the cross section which is available for conduction and the orientation and length of conduction path (Figure 2‑29). For isotropic disordered media, the ratio of the cross section available for conduction to the bulk cross section is equal to the bulk porosity, i.e. F is inversely related to porosity:

Figure 2‑29.II:

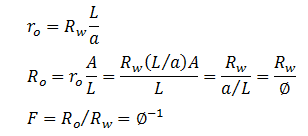
Figure 28.III:

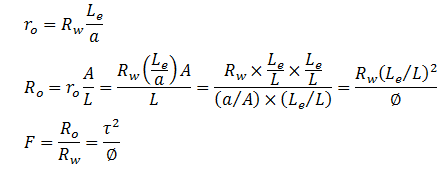
Where T is defined as tortuosity.

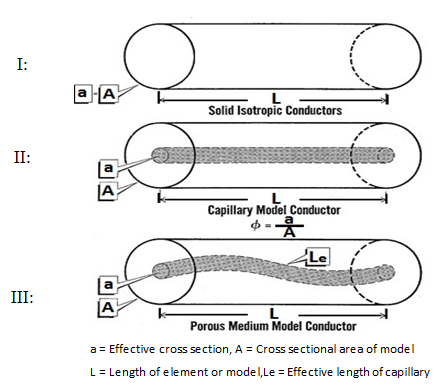
Figure 2-29: The Influence of Pore Structure on the Electrical Conductivity

Measurements showed that F varies more than just in inverse proportion to porosity. The first relationship between F and Φ was suggested by Archie (1942):

Where m is “cementation exponent” and its value is usually between 1.3 to 2.5 for various types of rocks. For clean and uniform size sands: a = 1 and m = 2. More general form of the Archie’s law is:

Where a is an intercept. Generally a logarithmic plot of F versus Φ is used to find a and m value for a special sample (Figure 2‑30).

According to the presented formula it can be shown that the following variables have effects on the resistivity of natural porous media:

• Temperature
• Water salinity
• Porosity
• Pore geometry
• Formation stress
• Rock composition
• Degree of cementation
• Type of pore system inter-crystalline
• Sorting and Packing (in particulate system)

The last six factors have effect through the influence on the conduction path. Confinement or overburden pressure may cause a significant increase in resistivity by blocking of some conduction paths and reduction in the cross sections which are available for flow.  This usually occurs in rocks with low porosity or that are not well cemented.  Older data was collected using measurements in unconfined core samples.  So to have the same condition as in the reservoir resistivity measurements and formation factors determination under confining pressures are recommended for improved analysis.

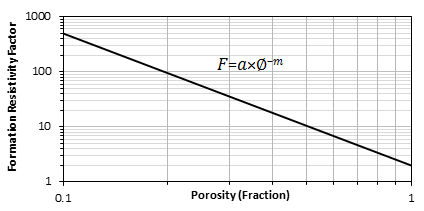
Figure 2-30: “Formation Resistivity Factor vs. Porosity

Several generalized relationships have been reported to relate F and Φ. The widely used ones are:

Equation	Investigator	Year	Comments
F = 0.62Φ-2.15	Winsauer et al	1952	data from 30 samples – 28 sandstones core plugs, one limestone plug, and one unconsolidated sand sample
F = 1.45Φ-1.54	Carothers	1968	Data from 793 sandstone reservoirs
F = 1.13Φ-1.73	Timur et al	1972	Data from 1833 sandstone samples
F = 2.45Φ-1.08	Porter and Carothers	1970	1575 F-φ data points from 11 wells from offshore California-Pliocene and four wells from offshore of Texas-Louisiana Miocene
F = 1.97Φ-1.29	Porter and Carothers	1970	720 F-φ data points from 11 wells from offshore California-Pliocene and four wells from offshore of Texas-Louisiana Miocene
F = 1.00Φ-2.04	Carothers	1968	Data from 188 carbonate samples
F = 1.00Φ-2.5	Schlumberger and Shell	1979	For compact rocks, low porosity and non-fractured carbonate
F = 1.97Φ-(1.87 + 0.019 / Φ)	Schlumberger and Shell	1979	For compact rocks, low porosity and non-fractured carbonate
F = 1 + 1.03(Φ-1.73 – 1)	Pérez-Rosales	1982	analytical relationship