Fundamentals of Fluid Flow in Porous Media
Chapter 2
Permeability
Permeability is a property of the porous medium that measures the capacity and ability of the formation to transmit fluids. The rock permeability, k, is a very important rock property because it controls the directional movement and the flow rate of the reservoir fluids in the formation. This rock characterization was first defined mathematically by Henry D’ Arcy in 1856. By analogy with electrical conductors, permeability represents reciprocal of residence which porous medium offers to fluid flow.
Poiseuille’s equation for viscous flow in a cylindrical tube is a well-known equation

Where:
- v = fluid velocity, cm/sec
- d = tube diameter, cm
- ∆P = pressure loss over length L,
- μ = fluid viscosity, centipoise
- L = length over which pressure loss is measured, cm
A more convenient form of Poiseuille’s equation is

If assume that the rock is consist of a lot of tube in different group with different radius, total flow rate from this system by using the equation (2‑18)
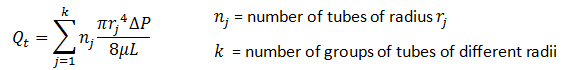
Example 2-4
Derive Poiseuille’s equation for viscous flow in a horizontal cylindrical tube.
Solution
Consider a horizontal flow in a circular pipe. Assume a disc shape element of the fluid in the middle of the cylinder that is concentric with the tube and with radius equal to rw and length equal to ∆L. The forces on the disc are due to the pressure on the upstream and downstream face of the disc and shear force over the rim of the element Figure 2‑20.
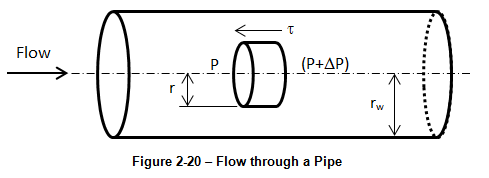
Figure 2-20: Flow through a Pipe
According to the steady state condition:

After simplification

According to the shear stress definition and using equation (2‑21) and then rearranged and integration on both sides
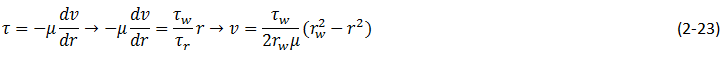
Maximum velocity at r=0 so

For viscous flow in the cylindrical tube

From (2‑21), (2‑24) and (2‑25)

d = 2rw , so after rearrangement
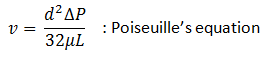
A cast of the flow channel in a rock formation is shown in (Figure 2‑21). It is seen that the flow channels are of varying sizes and shapes and are randomly connected. So it is not correct to use the Poiseuille’s equation for flow in the porous media.
In 1856, D’ Arcy (commonly known as Darcy) developed a fluid flow equation that has since become one of the standard mathematical tools of the petroleum engineer. He investigated the flow of water through sand filter for water purification. His experimental apparatus showed schematically in (Figure 2‑22) Darcy interpreted his observation so as to yield result essentially as following equation: Here Q represents the volume rate of flow of water downward through the cylindrical sand pack of cross sectional area A and height h and K is a proportionality constant. The sand pack was assumed to be fully saturated with water. Later investigator found that Darcy’s law could be extended to other fluid as well as water and that the constant of proportionality K could be written as ( K / μ ) . The final form of the Darcy equation for horizontal linear flow of an incompressible fluid is established through a core sample of length L and a cross-section of area A is Where: This is a linear law, similar to Newton’s law of viscosity, Ohm’s law of electricity, Fourier ‘s law of heat conduction, and Fick’s law of diffusion. Substituting the relationship u = Q/A, in equation (2‑28) results in The velocity, u, in Equation 2-29 is not the actual velocity of the flowing fluid but is the apparent velocity determined by dividing the flow rate by the cross-sectional area across which fluid is flowing. “Darcy” is a practical unit of permeability (in honor of Henry Darcy). A porous material has permeability equal to 1 Darcy if a pressure difference of 1 atm will produce a flow rate of 1 cm3/sec of a fluid with 1 cP viscosity through a cube having side 1 cm in length. Thus One Darcy is a relatively high permeability as the permeabilities of most reservoir rocks are less than one Darcy. In order to avoid the use of fractions in describing permeabilities, the term millidarcy is used. As the term indicates, one millidarcy, i.e., 1 md, is equal to one-thousandth of one Darcy. The negative sign in equation (2‑29) is necessary as the pressure increases in one direction while the length increases in the opposite direction. Permeability correlations Radial Version of Darcy’s Law Permeability and conductivity Example 2-5 Solution But because of isothermal flow, Q x ρ = Qb x ρb which “b” is as a “base condition”. For ideal gas at constant temperature: ρ = ρb ( ρ / ρb). Therefore Separating variable and integrating Define ̅P as ( P1 + P2 ) / 2 and ̅Q as flow rate at P = ̅P . Then: ̅PQ = PbQb. Substituting in equation (2‑32) There for flow rate of ideal gas could be found from the Darcy’s law for the incompressible fluid when the flow rate defined at the algebraic mean pressure. If you have any questions at all, please feel free to ask PERM! We are here to help the community.
Figure 2-21: Metallic cast of pore space in a consolidated sand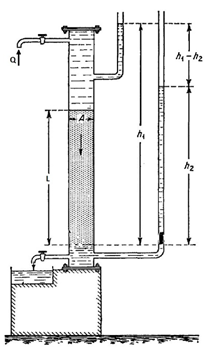
Figure 2-22: Schematic Drawing of Darcy Experiment of Flow of Water through Sand[2]




ADD TEXT TO SECTION (Section Not Complete)
Find the Darcy’s equation for isothermal flow of ideal gas.
Multiply both side of equation (2-28) by density so we have a mass flow equation: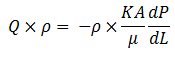



References
Questions?
