Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Relative Permeability

Comparison Between Capillary Pressure and Wettability

Similarities and analogs between capillary pressure and relative permeability curves for a two phase system is shown in Figure 2‑83.

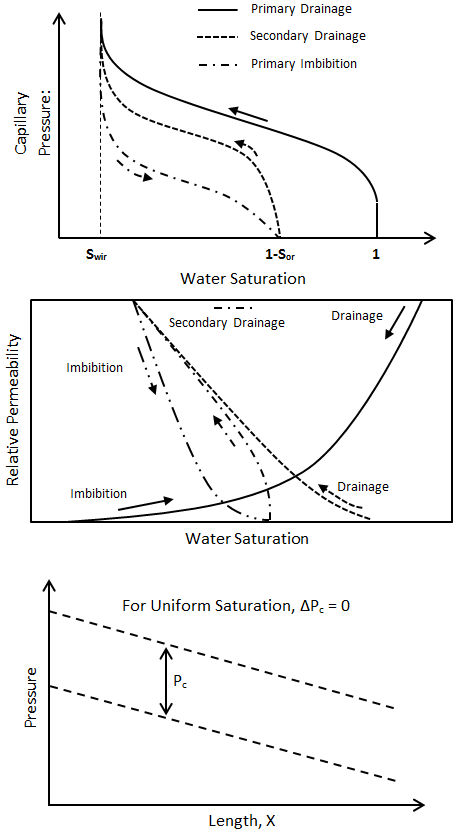
Figure 2-83: Comparison Between Capillary Pressure and Relative Permeability Curves

Fluid Distribution in Two Phase Flow

There are several important points regarding the distribution of fluids in porous media under two-phase flow condition.  The wetting phase seeks to maintain its continuum in the network of pore space involving the relatively small pore throats connecting pore bodies.  While the non-wetting phase seeks to maintain a continuum in a pore network involving the large pore throats.  As the non-wetting phase saturation increases, the wetting phase is “trapped” in the pore spaces accessible through relatively small pore throats.  However, as the non-wetting phase saturation decreases, k_rnw decreases (i.e. imbibition displacement) the wetting phase imbibes into relatively small pore throats and pore bodies in a hierarchical manner.  This results in the non-wetting phase being trapped in the relatively large pore bodies and large pore throats connecting trapped oil in pore bodies.  Also, in a water-wet formation at S*_or conditions, only water is flowing and k_ro(S*_or) is equal to zero.  However, if the formation is oil-wet, at S*_or conditions, k_ro(S*_or) is very small (10^-2) but never becomes zero because of wetting “film” flow.  Additionally, if the IFT is very small, there is a significant change in the relative permeability characteristics.

Relative Permeability Plots and Characteristics

The following summarises some important points about relative permeability and relative permeability curves for water-wet and oil-wet systems:

Water-wet system:

• k_rw = k_ro at S_w > 0.5,
• k_rw at S*_or is less than 0.3 (S*_or is the waterflood residual oil saturation),
• The amount of connate water saturation, S_wc, is usually greater than 20% (S_wc ≅ 20 to 25% PV) and has an effect on relative permeability behaviour,
• ( k_ro )_{primary drainage} > ( k_ro )_imbibition for the same S_w,
• The k_rw curve exhibits no hysteresis ( e.g., ( k_rw )_pd = ( k_rw )_imb ),
• As permeability increases, ( k_rw / k_ro ) becomes higher for a given saturation.

 

Oil-wet system:

• k_rw = k_ro at S_w < 0.5,
• k_rw ( S*_or ) > 0.5,
• S_wc has no effect on relative permeability behaviour, if S_wc < 20%,
• k_rw( S_w ) | _{primary drainage} > k_rw( S_w ) | _imbibition,
• k_ro curve exhibits no hysteresis,
• As permeability decreases, ( k_rw / k_ro ) becomes higher for a given water saturation.

 

For both oil and water-wet systems, the sum of ( krw + kro ) is always less than 1, when the same base permeability is used for normalization ( i.e., ( krw + kro ) < 1 ).  The main reasons for this are: 1) dendritic to flow pore space; 2) the connectivity of the network of each of the phases in the occupied pores is much smaller than that of the porous medium under single phase flow; and 3) pressure of immobile (trapped) fluids.