Fundamentals of Fluid Flow in Porous Media
Chapter 2
Multi-phase Saturated Rock Properties:
Capillary Pressure
The capillary pressure characteristics of a given reservoir will impact the choice of recovery method(s) and displacement mechanisms. For instance, the displacement of oil by water in a water-wet reservoir requires a totally different process compared to the displacement of oil by water in an oil-wet reservoir.
The capillary forces in a petroleum reservoir are the result of the combined effect of the surface and interfacial tensions of the rock and fluids, the pore size and geometry, and the wetting characteristics of the system. Any curved surface between two immiscible fluids has the tendency to contract into the smallest possible area per unit volume. This is true whether the fluids are oil and water, water and gas (even air), or oil and gas. When two immiscible fluids are in contact, a discontinuity in pressure exists between the two fluids, which depend upon the curvature of the interface separating the fluids. This difference existing across the interface is referred to as the capillary pressure (Pc). In other words Capillary pressure pc is defined as the pressure difference between the non-wetting phase and the wetting phase as a function of the (wetting phase) saturation. The displacement of one fluid by another in the pores of a porous medium is either aided or opposed by the surface forces of capillary pressure. As a consequence, in order to maintain a porous medium partially saturated with nonwetting fluid and while the medium is also exposed to wetting fluid, it is necessary to maintain the pressure of the nonwetting fluid at a value greater than that in the wetting fluid.
Consider Figure 2‑44 that a capillary tube in immersed in a beaker of water weather the oil is the other fluid.
- = Pressure in oil at point A’
- = Pressure in oil at point B
- = Pressure in water at point A
- = Pressure in water at point B
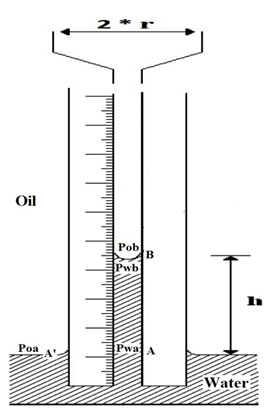
Figure 2-44: Pressure Relation in Capillary Tube
If the beaker is large the interface at point A’ is flat and capillary pressure is zero. Therefore

At the free water level in the beaker. The pressures at point B in oil and water phase, according to oil and water density, are:

The pressure difference across the interface at point B is:
This pressure difference (capillary pressure) is the reason of the curvature at the interface of the two liquid in the capillary tube. By increasing the capillary pressure this curvature increases and vice versa. The greater pressure is always on the concave side of the interface. Therefore the non-wetting phase in a porous material is at a higher pressure than the wetting phase. At the free level of the beaker (point A’) which interface is flat the capillary pressure is neglected.
According to the eq.(2‑77) the capillary pressure must be in equilibrium with gravitational forces if the fluids are in equilibrium and not flowing. Considering eq.(2‑67) and eq.(2‑77) the expression of capillary pressure in terms of surface force is:

This equation shows that capillary pressure is inversely proportional to the capillary tube diameter. This is the reason that by decreasing the capillary diameter, water column height and curvature in the interface increase (Figure 2‑45.a).
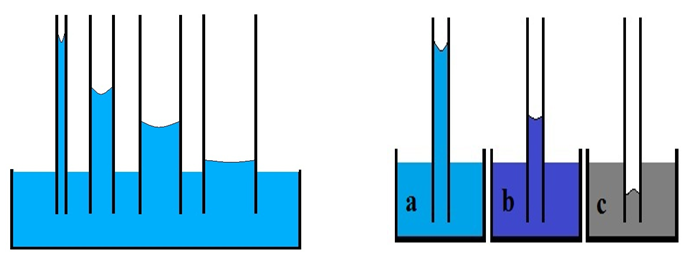
Figure 2-45: Dependency of Water Column to A) Capillary Radius, B) Wettability
Figure 2‑45.a shows the dependency of the equilibrium liquid column to the capillary tube radius. In addition to change the capillary radius, change in wetting characteristic changes the liquid column height, such that the greater wettability (adhesion tension) the greater equilibrium height obtained. In Figure 2‑45.b wettability decreases from ‘a’ to ‘c’ (liquid ‘c’ is non-wet).
The interfacial phenomena described above for capillary tubes also exist when bundles of interconnected capillaries of varying sizes exist in a porous medium. The capillary pressure that exists within a porous medium between two immiscible phases is a function of the interfacial tensions and the average size of the capillaries which, in turn, controls the curvature of the interface.
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
