Fundamentals of Fluid Flow in Porous Media
Chapter 2
Relative Permeability
Three Phase Relative Permeability: Effects of Low IFT or Nca on Relative Permeability
In the literature, many researchers agree that as the interfacial tension (IFT) is reduced, relative permeabilities increases. There are people who believe that the relative permeability relationship with saturation is a linear function and there are people who report otherwise.
Harbert noticed that the flow of low IFT fluids differs from that of conventional gas-oil-water systems in both sandstones and carbonates. He found that both water and oil relative permeability curves were found to shift upward, indicating that the two phases interfere less with each other as IFT is reduced In this figure, kro appears to be a straight line while krw still maintains its curvature ( N in the figure is the capillary number, which is the same as Nca ). Also, the change in krw as IFT changes is not significant. However, Sor did change; in this case it becomes less than 10%. For the lower capillary number, the water relative permeability curve is a function of saturation (no hysteresis). Harbert also mentioned that at the same Nca and IFT, a less permeable core has a higher residual saturation. This is expected because a core that was less permeability has pores that are not well connected, and the invading fluid cannot easily displace oil from these pores. Foulser et al. proposed a model in 1992 for relative permeability at high capillary number for the flow of two or more phases[20]. This model allows the residual oil saturation to be reduced as the capillary number is increased. As mentioned before, many people conventionally assumed that relative permeabilities are linear functions of saturations for low IFT fluids. However, this model assumes that relative permeability is non-linear, as shown in some reports. It also assumes that the flow of two or three phases can be represented by the flow of droplets of fluid through the pore network. The geometry of the pore network was assumed to consist of capillary tubes. The relative permeability can then be derived as a function of saturation according to this equation, And Where, krα = relative permeability of phase α korα = end point relative permeability of phase α μα= viscosity of phase α ƒβ = fractional flow of phase β N = number of droplets N defines the droplet size relative to the capillary tube length. When N = 1 flow is segregated and the relative permeabilities are linear functions of saturation. As N approaches infinity, a “mixed flow” regime is created, in which the droplet size is very small compared to the tube length, giving the relative permeabilities as a function of saturation. In this model the relative permeabilities are a function of phase viscosities as well as saturations. [19] Harbert, L.W., “Low Interfacial Tension Relative Permeability”, SPE 12171. [20] Foulser, R.W.S., Goodyear, S.G. and Sims, R.J., “Two- and Three-Phase Relative Permeability Studies at High-Capillary Numbers”, SPE 24152. If you have any questions at all, please feel free to ask PERM! We are here to help the community.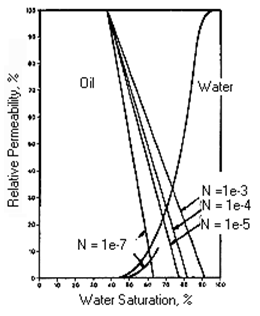
Figure 2-91: Effect of Capillary Number on Relative Permeability (After 9)


References
Questions?
