Fundamentals of Fluid Flow in Porous Media
Chapter 2
Multi-phase Saturated Rock Properties:
Surface and Interfacial Surface Tension
In dealing with multiphase systems, it is necessary to consider the effect of the forces at the interface when two immiscible fluids are in contact. When these two fluids are liquid and gas, the term surface tension is used to describe the forces acting on the interface. Surface tension is a property of the surface of a liquid that allows it to resist an external force and liquid surface acts like a thin elastic sheet. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water. When the interface is between two liquids, the acting forces are called interfacial tension.
The cohesive forces among the liquid molecules are responsible for this phenomenon of surface tension. In the bulk of the liquid, each molecule is pulled equally in every direction by neighboring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have the same other molecules on all sides of them and therefore are pulled inwards. This creates some internal pressure and forces liquid surfaces to contract to the minimal area. The unbalanced attraction force between the molecules creates a membrane like surface with a measurable tension, i.e., surface/interfacial tension (Figure 2‑33).
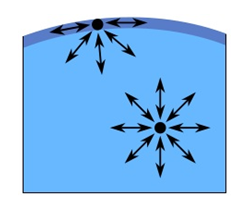
Figure 2-33: Illustration of Surface Tension (surface molecules pulled toward liquid causes tension in surface)
A certain amount of work is required to move a water molecule from within the body of the liquid through the interface. This work is frequently referred to as the free surface energy of the liquid. Free surface energy may be defined as the work necessary to create a new unit area of the surface. The interfacial/surface tension is the force per unit length required to create new surface which is numerically equal to the surface energy. The surface or interfacial tension has the units of force per unit of length, e.g., dynes/cm, and is usually denoted by the symbol σ.
Simple models for interfacial tension Determination (IFT)
Soap Film: Consider a liquid film enclosed by a wire loop (Figure 2‑34.a) where one side of the loop is allowed to slide back and forth. A force (f) is applied to counter the contractive force due to the surface tension of the liquid. Working against the surface tension an incremental increase in the force will do work δW in pulling the slide out a distance dx:

We define the Surface Tension in terms of this force such that:

Where, ‘L’ is the length along the slide and the factor of ‘2’ is required to account for the film’s two sides. Then we relate the surface tension to the change in area (A) of the film via:

Where, ‘dA’ is the increase in area of the surface of the liquid film.
Soap Bubble: Consider a soap bubble of radius r, (Figure 2‑34.b), where energy is described by:

Where, 4πr2 is the area of the bubble as a sphere. If the radius is decreased by dr, then the change in surface energy is:

Since shrinking decreases the surface energy, the tendency to do so must be balanced by a pressure difference across the film, ΔP, such that the work against this pressure difference is equal to the decrease in surface free energy. In other words:

So:

Where, ΔP = (Inside pressure) – (Outside pressure). Therefore, the smaller the soap bubble, the larger the air pressure inside compared to outside.
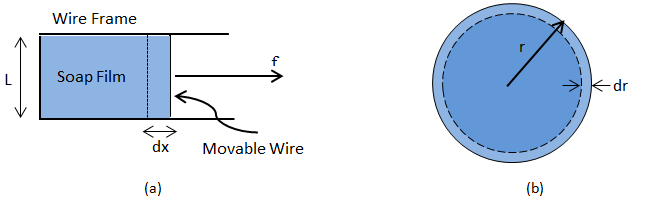
Figure 2-34: Simplified Models for Interfacial Tension Determination
Capillary rise Method: This methodology employs a small bore capillary which is inserted into the liquid whose surface tension is to be determined (Figure 2‑35). The height to which the liquid rises in the tube is proportional to the surface tension. Assuming the radius of the capillary tube is r, the total upward force Fup, which holds the liquid up, is equal to the force per unit length of surface times the total length of surface, or

Where ∅ is contact angle.
The upward force is counteracted by the weight of the water, which is equivalent to a downward force of mass times acceleration, or
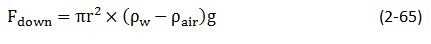
Where
- h = height to which the liquid is held, cm
- g = acceleration due to gravity, cm/sec2
- ρw = density of water, gm/cm3
- ρair = density of gas, gm/cm3
Density of air is negligible compared to the water density.
Equating eq.(2‑64) and eq.(2‑65) and solving for the surface tension gives:

And for water-oil system:

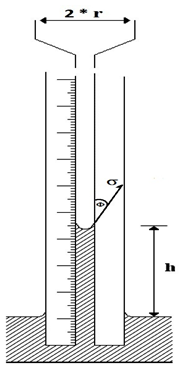
Figure 2-35: Pressure relations in capillary tubes
WETTABILITY >>
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
