Fundamentals of Fluid Flow in Porous Media

Chapter 3

Fick’s Law of Binary Diffusion

The description of diffusion involves a mathematical model based on a fundamental hypothesis or ‘‘law’’.  Imagine two large bulbs connected by a long thin capillary (Figure 3‑1). Both of bulbs are at the same pressure and temperature but are filled with two different gases (N₂ upper bulb and CO₂ lower one). The concentration of the carbon dioxide in the initially N₂ filled bulb is measured with time to find how fast these two gases will mix. The concentration of CO₂ varies linearly with time (Figure 3‑1). So the amount of CO₂ transferred could be determined from this graph at each time step. Carbon dioxide flux is defined as follows:

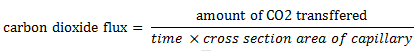
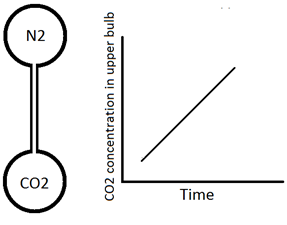
Figure 3-1: Simple Diffusion Experiment

We can assume that the flux is proportional to the gas concentration difference and we can recognize that increasing the capillary tube length will decrease the flux, so:

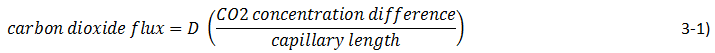
The new proportionality constant D is the diffusion coefficient. Its introduction implies a model for diffusion, the model often called Fick’s law. There is a similarity between Fick’s law and Ohm’s law for flux of electrons:

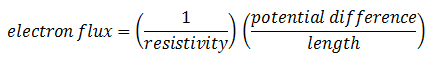
The diffusion coefficient D is proportional to the reciprocal of the resistivity. So the general form of Fick’s law is

Where, j is the diffusion flux, and the minus appears because of the opposite directions of diffusion flux and concentration gradient.

From eq. (3‑2), we see that D has units ( L² / T ). Since Fick’s law is derived for molecules moving in Brownian motion, D is a molecular diffusion coefficient, which is called D_o to be specific. The intensity (energy and freedom of motion) of these Brownian motions controls the value of D. Thus, D depends on the phase (solid, liquid or gas), temperature, and molecule size.

It should be considered that the Fick’s Law could not be applied when the capillary is very thin or two gases react.

Parallel to Fourier’s law for heat conduction Fick’s second law is developed as;

for one dimensional unsteady state diffusion, and for the constant area, A, it becomes the more known Fick’s second law equation:

This equation can be applied only for isotropic media and when the potential for diffusion is only given by concentration gradients.  The diffusion coefficient is also independent of concentration.

Example 3-1

Find the diffusion flux and concentration profile in a steady diffusion across a thin film.

Solution

The objective is to determine how much solvent moves across the film and how the solvent concentration changes within the film. On each side of the film is a well-mixed solution of one solvent. The solvent diffuses from the fixed higher concentration, located at x < 0 on the left-hand side of the film, into the fixed, less concentrated solution, located at x > l on the right-hand side. As the first step mass balance on a thin layer located at some arbitrary position x within the film is written:

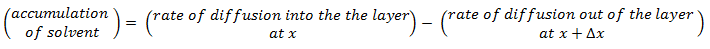
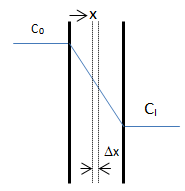
Figure 3-2: Diffusion Across a Thin Film

Because the process is in steady state, the accumulation is zero. The diffusion rate is the diffusion flux times the film’s area A. Thus

Divide this equation by the layer volume: A x Δx

Combining eq. (3‑6) with Fick’s law equation (3‑2) yields the following equation:

Where C = solvent concentration in the layer. There are two boundary conditions for this differential equation:

Analytical solution of eq. (3‑7), according to these two boundary conditions, will be the concentration profile:

The resulted solution for the concentration profile shows that the profile is independent of the diffusion coefficient. Base on the Fick’s law the diffusion flux can be found by differentiation of concentration profile: