Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Multi-phase Saturated Rock Properties:

Wettability

There exists a surface tension between a fluid and a solid, in the same way that a surface tension exists between two immiscible fluids. Wettability is defined as the tendency of one fluid to spread on or adhere to a solid surface in the presence of other immiscible fluids. This spreading tendency can be expressed more conveniently by measuring the angle of contact at the liquid-solid surface. This angle, which is always measured through the liquid to the solid, is called the contact angle θ_c that is known also as wetting angle. The contact angle cos θ_c has achieved significance as a measure of wettability. As shown in Figure 2‑36, as the contact angle decreases, the wetting characteristics of the liquid increase. Complete wettability would be evidenced by a zero contact angle, and complete non-wetting would be evidenced by a contact angle of 180°. There have been various definitions of intermediate wettability but, in much of the published literature, contact angles of 60° to 90° will tend to repel the liquid. When one fluid preferentially covers the surface, it is called the wetting fluid, and the other fluid is called the non-wetting fluid. The origin of these surface tensions arises in the different strengths of molecular level interactions taking place between the pairs of fluids. For example a quartz sandstone grain generally develops greater molecular forces between itself and water than between itself and oils. Clean sandstones are therefore commonly water wet.

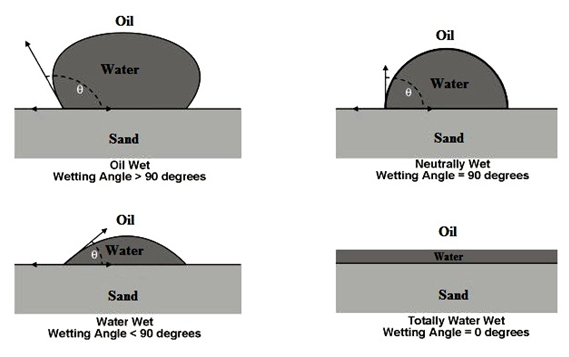
Figure 2-36: Illustration of Wettability

When two fluids are in contact with a solid surface, the equilibrium configuration of the two fluid phases (for example air and water) depends on the relative values of the surface tension between each pair of the three phases (Figure 2‑37). Each surface tension acts upon its respective interface, and define the angle θ_c at which the liquid contacts the surface. Equilibrium considerations allow us to calculate the wetting angle from the surface tensions:

This equation is known as Young’s equation (1805).

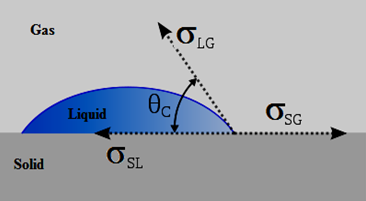
Figure 2-37: Equilibrium of Forces at a Liquid-Gas-Solid Interface

The problems with using the Young’s equation approach include:

• The values of σ_SL and σ_SG cannot be measured independently in an experiment,
• Surface roughness effects are not considered.

To account for surface roughness it was suggested by (Wenzel, 1936):

Where, θ_app is the apparent contact angle and f_r is a roughness parameter defined as the ratio of the true area of the solid-liquid interface to the apparent area of the solid-liquid interface.  f_r  > 1 for any real surface.

Table 2 shows some contact angles and surface tensions for common fluids in the hydrocarbon industry.

Interface	Contact angle (θc)	cosθc	Interfacial Tension (dyne/cm)
Air-Water	0	1.000	72
Oil-Water	30	0.866	48
Air-Oil	0	1.000	24
Air-Mercury	140	-0.756	480