Fundamentals of Fluid Flow in Porous Media
Chapter 2
Multi-phase Saturated Rock Properties:
Phase Trapping: Jamin Effect
The Jamin Effect In Figure 2‑72 assume the system is static with different pressure existence between point A and B because of capillary forces. The static pressure difference must be exceeded for flow to occur, in other words the static pressure difference, PA – PB, must be overcome to initiate flow. In Figure 2‑72.a the capillary tube size varies and therefore the radius is smaller on one side of the drop than on the other. Figure 2‑72.b shows a situation that the contact angle is different on the two sides of the drop, which could result, for example, if the drop displaced in one direction that there will have one Advancing contact angle and one Receding. In Figure 2‑72.c a gas drop is trapped between water and oil. An assumption is made that the pressure within the oil or gas drop is constant from one end to the other end of drop. With this assumption we have Subscripts A and B are the values are determined for the interfaces at point A and B. Application of this equation in Figure 2‑72.a, b, c yields the following forms. Figure 2‑72.a: Assume θA = θB the pressure difference at static condition is If rA > rB then PA > PB and a pressure drop exists in the direction from point A to point B. this gradient would have to be exceeded to induce flow into the narrower part of the capillary constriction. Figure 2‑72.b: For an advancing contact angle at point B and a receding at point A, θA > θB and cosθA < cosθB. Again PA > PB and a pressure gradient exist in the potential direction of flow at static, or trapped, condition. Figure 2‑72.c: In this case IFT and contact angles are different at the two interfaces because of different fluid systems. If σgwcosθA < σgocosθB a pressure drop exists from point A to point B when this system is static. If you have any questions at all, please feel free to ask PERM! We are here to help the community.

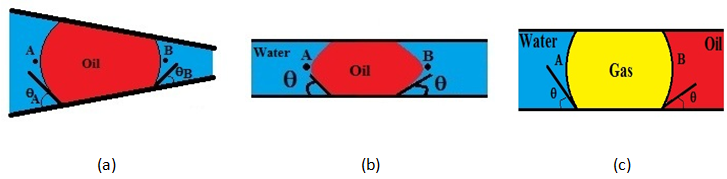
Figure 2-72: Trapping of a Droplet in a Capillary Tube



References
Questions?
