Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
Fluid Properties in Miscible Displacement: Fluid Density
Knowledge of relative density of the fluid and fluid mixtures is important for miscible displacement design. Gravity override or underride and fingering are usual phenomena during displacement process that are results of density difference between displaced and displacing liquids. Detailed description of these phenomena will be explained in the subsequent sections. Crude oils tend to have specific gravities in the 0.80 to 0.95 range at 60°F. Density is a function of pressure and temperature and can be estimated at the reservoir condition. During the solvent injection two different fluids (oil and solvent) with different densities mix together. McCain An estimate of liquid density can be calculated on the basis of a mole-averaged sensitivity of pure components as follows: Where, Xi = mole fraction of component I in the mixture, ρi = Mole density of component i, ρmix = Mole density of the mixture. Mole density could be converted to mass density by multiplication by the average molecular weight of the mixture. Gas density can be calculated with the EOS: Where, P = Pressure, V = Specific volume, T = Temperature, R = Gas constant, 8.314 ( m3.Pa ) / ( K.mol ) Z = Compressibility factor that shows the deviation from ideal gas law. Compressibility factor is a function of reduced temperature ( Tr ) and reduced pressure ( Pr ) that are defined as For a mixture of gases using the ideal gas mixture assumption critical pressure and temperature are defined as follow and are named pseudocritical pressure ( Ppc ) and pseudocritical temperature ( Tpc ): Where, n = number of components, Xi = mole fraction of component “i”. [1] “The properties of Petroleum Fluids”, McCain Jr., W.D., PennWell Publishing Co., Tulsa, OK (1973) If you have any questions at all, please feel free to ask PERM! We are here to help the community.


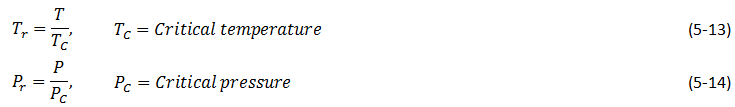

References
Questions?
