Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
Fluid Properties in Miscible Displacement: Macroscopic Displacement Efficiency
Gravity Effect in Dipping Reservoirs[50]
In some reservoirs with dip, gravity can be used to advantage to improve sweepout and oil recovery. This is achieved by injecting the solvent updip and producing the reservoir at a rate low enough for gravity to keep the less dense solvent segregated from the oil, suppressing fingers of solvent as they try to form. For example if oil were displaced from a reservoir by injecting a less dense, more mobile solvent up-dip, gravity would tend to stabilize the displacement front. That is, if the displacement velocity were sufficiently low, gravity forces would act to prevent the formation of fingers at the solvent/oil interface. Similarly, in water flood down-dip injection of water can work to stabilize the interface between the water and oil bank interface. There are some criteria to have a stable gravity displacement. With the same strategy that was used to find the criteria for grows of the viscous fingers (eq.(5‑40)), in the following paragraphs we will try to find the criteria for stable displacement in a dipping reservoir.
Consider a displacement in a down-dip direction in which the reservoir dip is at an angle t to the horizontal. Assume that the interface is sharp with only displacing fluid flowing ahead of the front. For miscible displacement that means there is no mixing at the interface. Assume a small perturbation, finger, or protrusion has formed at the interface (Figure 5‑41). The same as viscous fingering the objective of the analysis is the determination of conditions under which the perturbation will remain stable or will grow in magnitude, leading to an unstable interface.
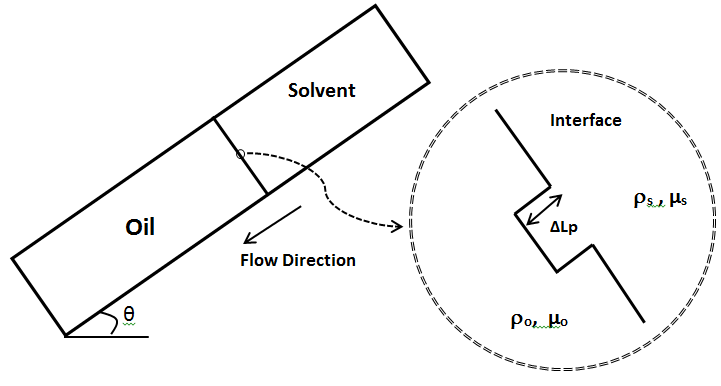
Figure 5-41: Model for Determining Stability Criterion in a Dipping Reservoir
If the pressure of the displaced phase (oil) just at the interface of the finger is higher than the displacing (solvent) pressure the finger will remain stable.
According to Darcy’s equation solvent and oil pressure (Ps and Po) just at the perturbation face could be find as: (see Figure 5‑41)

Where,
po = Reference pressure at the point of the unperturbed interface.
ΔLp = Length of perturbation.
In these equation on the right hand side of equations the first term is the pressure at the unperturbed interface, second term is the gravity pressure in the flow direction caused by the oil or solvent column and the third term is the pressure difference caused by flow.
For the interface to remain stable:

Substituting eqs. ( (5‑44)and(5‑45) ) into eq. ((5‑46)):

using eq.(5‑47) critical velocity as the maximum velocity at which the interface will remain stable, defined as:

In customary units, and if ks = ko and M = μo / μs
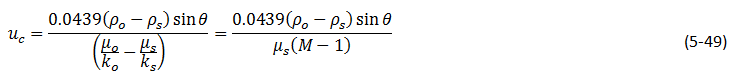
Where,
ρ is in ib/ft3, µ in cp, k in Darcies, and uc in feet per day.
In derivation of eq. (5‑49) we assumed that there is a sharp interface between displaced and displacing fluid, while in miscible displacement there is a mixing zone between oil and solvent that solvent concentration change from zero to pure solvent in this zone. For this condition ust is defined as the maximum flow velocity for a completely stable displacement.
The velocity, ust, is called “stable rate”. Below this velocity the miscible displacement is completely stable throughout the transition zone.
ust is more stringent criterion. If the actual displacement velocity, u, is greater than uc , the displacement is unstable and solvent fingers into the oil. If u < ust the displacement is completely stable. However if ust < u < uc , a portion of transition zone is unstable and fingers into the oil. At this later condition there is no instability causing the pure solvent to finger into the oil because the displacement is below the critical rate, and an efficient displacement of oil by the undiluted solvent still result for continuous solvent injection. However, the fingering within a portion of solvent/oil transition zone causes more rapid dilution of a solvent slug by mixing than would be the case with a completely stable displacement.
The following equation shows a relation between stable rate and critical rate:

Example 5‑7
A miscible flood displacement is to be conducted in a laboratory experiment in which one glycerol/brine solution is displaced vertically downward by a second solution having a different concentration of glycerol. Liquid properties are as follows:
Properties
Liquid # 1 (Displacing (D))
Liquid #2 (Displaced (d))
NaCl content, (gr/liter)
30.00
20.00
Glycerol content, (gr/liter)
650
700
Density, (gr/cm3) at 77°F
1.1551
1.1609
Viscosity, (cp) at 77°F
7.4
1.3
The liquid Darcy velocity is to be 0.237 ft/D. porosity of the porous medium is 0.206 and permeability is 303 md.
Determine whether viscous fingering will occur?
Calculate μst / μc
Solution
Equation (5‑48) is applicable for calculation of nc:

Because the planned velocity of 0.237 ft/D >> uc , the flow will be unstable and viscous fingering will occur.
Eq. (5‑50) is applicable:
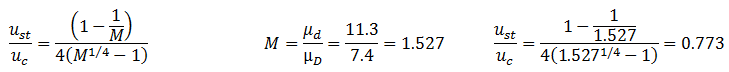
Fluid mixing results in an even smaller maximum velocity for stable flow.
As this example showed, the critical velocity is so low and most of the time, in field application, injection velocity is higher than this critical value. Several solutions were suggested to increase the final recovery of the miscible flood. Kantzas et al.[1] proposed a method to increase the final recovery of a vertical miscible performance using cyclic pressure pulsing. This method is illustrated in the next section.
References
[1] “Optimization of Vertical Miscible Flood Performance through Cyclic Pressure Pulsing”, Kantzas, A., Marentette, D.F., See, D., Adamache, I., Mclntyre, F.I., Sigmund, P.M., JCPT, vol. 33, July 1994
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
In some reservoirs with dip, gravity can be used to advantage to improve sweepout and oil recovery. This is achieved by injecting the solvent updip and producing the reservoir at a rate low enough for gravity to keep the less dense solvent segregated from the oil, suppressing fingers of solvent as they try to form. For example if oil were displaced from a reservoir by injecting a less dense, more mobile solvent up-dip, gravity would tend to stabilize the displacement front. That is, if the displacement velocity were sufficiently low, gravity forces would act to prevent the formation of fingers at the solvent/oil interface. Similarly, in water flood down-dip injection of water can work to stabilize the interface between the water and oil bank interface. There are some criteria to have a stable gravity displacement. With the same strategy that was used to find the criteria for grows of the viscous fingers (eq.(5‑40)), in the following paragraphs we will try to find the criteria for stable displacement in a dipping reservoir.
Consider a displacement in a down-dip direction in which the reservoir dip is at an angle t to the horizontal. Assume that the interface is sharp with only displacing fluid flowing ahead of the front. For miscible displacement that means there is no mixing at the interface. Assume a small perturbation, finger, or protrusion has formed at the interface (Figure 5‑41). The same as viscous fingering the objective of the analysis is the determination of conditions under which the perturbation will remain stable or will grow in magnitude, leading to an unstable interface.

Figure 5-41: Model for Determining Stability Criterion in a Dipping Reservoir
If the pressure of the displaced phase (oil) just at the interface of the finger is higher than the displacing (solvent) pressure the finger will remain stable.
According to Darcy’s equation solvent and oil pressure (Ps and Po) just at the perturbation face could be find as: (see Figure 5‑41)

Where,
po = Reference pressure at the point of the unperturbed interface.
ΔLp = Length of perturbation.
In these equation on the right hand side of equations the first term is the pressure at the unperturbed interface, second term is the gravity pressure in the flow direction caused by the oil or solvent column and the third term is the pressure difference caused by flow.
For the interface to remain stable:

Substituting eqs. ( (5‑44)and(5‑45) ) into eq. ((5‑46)):

using eq.(5‑47) critical velocity as the maximum velocity at which the interface will remain stable, defined as:

In customary units, and if ks = ko and M = μo / μs
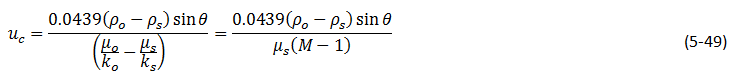
Where,
ρ is in ib/ft3, µ in cp, k in Darcies, and uc in feet per day.
In derivation of eq. (5‑49) we assumed that there is a sharp interface between displaced and displacing fluid, while in miscible displacement there is a mixing zone between oil and solvent that solvent concentration change from zero to pure solvent in this zone. For this condition ust is defined as the maximum flow velocity for a completely stable displacement.
The velocity, ust, is called “stable rate”. Below this velocity the miscible displacement is completely stable throughout the transition zone.
ust is more stringent criterion. If the actual displacement velocity, u, is greater than uc , the displacement is unstable and solvent fingers into the oil. If u < ust the displacement is completely stable. However if ust < u < uc , a portion of transition zone is unstable and fingers into the oil. At this later condition there is no instability causing the pure solvent to finger into the oil because the displacement is below the critical rate, and an efficient displacement of oil by the undiluted solvent still result for continuous solvent injection. However, the fingering within a portion of solvent/oil transition zone causes more rapid dilution of a solvent slug by mixing than would be the case with a completely stable displacement.
The following equation shows a relation between stable rate and critical rate:

Example 5‑7
A miscible flood displacement is to be conducted in a laboratory experiment in which one glycerol/brine solution is displaced vertically downward by a second solution having a different concentration of glycerol. Liquid properties are as follows:
| Properties | Liquid # 1 (Displacing (D)) | Liquid #2 (Displaced (d)) |
| NaCl content, (gr/liter) | 30.00 | 20.00 |
| Glycerol content, (gr/liter) | 650 | 700 |
| Density, (gr/cm3) at 77°F | 1.1551 | 1.1609 |
| Viscosity, (cp) at 77°F | 7.4 | 1.3 |
The liquid Darcy velocity is to be 0.237 ft/D. porosity of the porous medium is 0.206 and permeability is 303 md.
Determine whether viscous fingering will occur?
Calculate μst / μc
Solution
Equation (5‑48) is applicable for calculation of nc:

Because the planned velocity of 0.237 ft/D >> uc , the flow will be unstable and viscous fingering will occur.
Eq. (5‑50) is applicable:
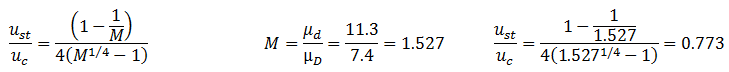
Fluid mixing results in an even smaller maximum velocity for stable flow.
As this example showed, the critical velocity is so low and most of the time, in field application, injection velocity is higher than this critical value. Several solutions were suggested to increase the final recovery of the miscible flood. Kantzas et al.[1] proposed a method to increase the final recovery of a vertical miscible performance using cyclic pressure pulsing. This method is illustrated in the next section.
References
[1] “Optimization of Vertical Miscible Flood Performance through Cyclic Pressure Pulsing”, Kantzas, A., Marentette, D.F., See, D., Adamache, I., Mclntyre, F.I., Sigmund, P.M., JCPT, vol. 33, July 1994
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
