Fundamentals of Fluid Flow in Porous Media
Chapter 3
Diffusion Coefficient
The diffusion coefficient was introduced as a proportionality constant, the unknown parameter appearing in the Fick’s law. Often Do is used as the molecular diffusion nomenclature. Mass fluxes and concentration profiles in many situations can be found using Fick’s law equation and, most of the time, the results contained the diffusion coefficient as an adjustable parameter. There exist four important definitions of the diffusion coefficient depending on the nature of the diffusion process Overall Diffusion Coefficient (Mutual Diffusivity): It is denoted by DAB, and it refers to the diffusion of one constituent in a binary system (A and B). For liquids, it is common to refer to the limit of infinite dilution of A in B using the symbol, D°AB. Assume a bitumen-solvent vertical system where solvent is on the top of the bitumen. The diffusion rate of solvent through a unit area is described by eq. (3‑2) as follows: Where, Dos = Diffusion coefficient of solvent, Cs = Solvent concentration, y = Vertical direction. As solvent diffuses into the bitumen, a diffusion flux occurs for oil molecules toward the solvent: Where, Dob = Diffusion coefficient of solvent, Cb = Solvent concentration. According to the volume conservation in the system, the diffusion flux of bitumen should be equal to the solvent flux, but in opposite direction: Also: From eqs ((3‑13) to (3‑15)): The overall diffusion coefficient Dbs is a material property that describes the mobility of either component in the mixture. Self Diffusion Coefficient: It is denoted by DA’A and is the measure of mobility of a species in itself. Also when we have a binary system where A and B are the less mobile and more mobile components respectively, their self-diffusion coefficients can be used as rough lower and upper bounds of the mutual diffusion coefficient in some systems. That is, DA’A < DAB < DB’B. Intrinsic Diffusion Coefficient: When there is a considerable difference between the molecule size of solvent and oil, for example in the previous system of solvent-bitumen, during diffusion of solvent into bitumen (in the previous system), the small solvent molecules tend to diffuse faster than the large molecules of bitumen. The intrusion of solvent molecules into bitumen causes a buildup of pressure in bitumen part. This pressure gradient causes a bulk flow of bitumen solution toward the solvent-rich part. In this situation the net flow of solvent is the sum of the diffusional flux of solvent Where, Db = Bitumen Intrinsic Diffusion Coefficient, Ds = Solvent Intrinsic Diffusion Coefficient, u = Bulk Flow Velocity Intrinsic diffusion coefficient is dependent on the concentration as the overall diffusion coefficient. Bulk flow velocity could be found from eq. (3‑17): When there is not much difference between the molecule sizes of solvent and oil the net flow velocity is almost zero, because of the equality between intrinsic diffusion coefficient of oil and solvent. Although for solvent-bitumen system which intrinsic diffusion coefficient of solvent is higher than bitumen, because of smaller molecular size, bulk flow will be most significant. Eq. (3-19) describe the volume conservation of solvent in a solvent-bitumen system: But the net flux of solvent was found with eq. (3‑12). Equal eq. (3‑12) with eq. (3‑19), with attention to eq. (3‑16) to find the following equation: Substituting eq. (3‑18), for ‘u’, into the eq. (3‑20) will be ended with the following relation between the overall and intrinsic diffusion coefficient: So the overall diffusion coefficient value is equal to the intrinsic diffusion coefficient of solvent in pure bitumen ( Cs = 0 ) and intrinsic diffusion coefficient of bitumen in pure solvent ( CB = 0 ). Ds and Db are concentration dependent as Dbs, but there is no way to find the equation of this dependency other than with experiment. Most of the time a linear relationship between the intrinsic and concentration is assumed. The minimum value of the solvent intrinsic diffusion coefficient is the overall diffusion coefficient when solvent concentration is zero and the maximum is solvent self-diffusion coefficient, and the same for bitumen. By knowing the minimum and maximum of the intrinsic diffusion coefficient of bitumen and solvent and assumption of a linear relationship between these coefficients and concentration a relation between overall diffusion coefficient and concentration could be found using eq. (3‑21). Figure 3‑3 shows a result for such calculation. Regarding eq. (3‑21) and Figure 3‑3, the overall diffusivity reaches a maximum at an intermediate concentration. During the experimental measurement of diffusion coefficient, what we find is the overall diffusion coefficient. Tracer Diffusivity: Denoted by DA’B is related to both mutual and self-diffusivity. It is evaluated in the presence of a second component B, using a tagged isotope of the first component. In the dilute range, tagging A merely provides a convenient method for indirect composition analysis. As concentration varies, tracer diffusivities approach mutual diffusivities at the dilute limit, and they approach self-diffusivities at the pure component limit. In some cases the diffusion coefficient can be reasonably taken as constant (e.g. dilute solutions) while, in some others it depends very markedly on concentration. If you have any questions at all, please feel free to ask PERM! We are here to help the community.





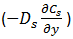 and the flux of solvent displaced by bulk flow ( uXs ), which ‘u’ is measured in the direction of ‘y’. According the volume balance solvent, net flow should be equal to the bitumen net flow with diffusion and bulk flow:
and the flux of solvent displaced by bulk flow ( uXs ), which ‘u’ is measured in the direction of ‘y’. According the volume balance solvent, net flow should be equal to the bitumen net flow with diffusion and bulk flow:





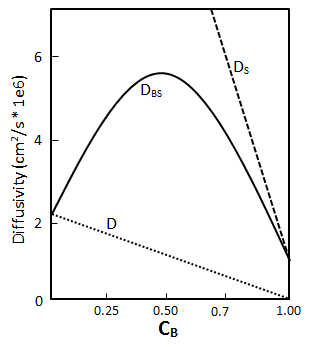
Figure 3-3: Prediction Overall Diffusion from Intrinsic DiffusionReferences
Questions?
