Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Relative Permeability

Two Phase Relative Permeability Literature Survey

Experimental Research and Relative Permeability Predictions

In the last forty years, there have been many experimental investigations on relative permeability measurements. Shankar (1979) gives a detailed discussion on the experimental techniques that apply for these measurements. He also gives a review of the experimental work done and of some attempts to predict relative permeability up until the early seventies. McCaffery (1973) also gives a detailed discussion on the proposed methods of prediction of relative permeability characteristics up until that time.

There are certain factors that influence the experimental measurements of permeability and the relative permeability characteristics in general. These factors are:

• The Boundary or End Effects
• The Hysteresis Effect
• The Migration or Partial Water Saturation Effect
• The Flow Rate Effect
• The Effect of Gas Expansion

as they were discussed by Geffen et al (1951)and Shankar (1979).

In later research works, the effect of many parameters on relative permeability and/or effective permeability characteristics was examined. These parameters are:

• Wettability
• Capillary number
• Pore geometry
• Heterogeneity of the system
• Anisotropy of the system
• Fluid viscosity
• Interfacial tension (IFT)
• Temperature

One parameter of major importance in relative permeability characteristics is wettability. McCaffery (1973) examined its effect on the relative permeability characteristics of porous media made from Teflon using different fluids in various wetting conditions. Shankar (1979) examined the effect of wettability in sandstones and he reported experimental results that cover a range of wetting conditions as well.  Some results are shown in Figure 2-83.

The effect of interfacial tension on relative oil/water permeabilities for the case of consolidated porous media has been investigated by Amaefule and Handy (1982). The samples used were fired Berea cores. They also tested temperature effects both in steady and unsteady state cases. They have found that oil/water relative permeabilities are greatly affected at IFT values less than 0.1 mN/m. They provide some empirical equations that fit their data.

Keelan (1976) examined the gas-water relative permeability characteristics during imbibition. He reported plots of relative permeability as a function of saturation and its variations due to pore geometry. He correlated his results using the end-point relative permeability and the trapped gas saturation.

Early studies by Johnson et al (1959) provided the first calculations of relative permeability based on data from displacement experiments. Honarpour et al (1982) report empirical equations for the estimation of two-phase relative permeability in consolidated rocks.

Torabzadeh and Handy (1984) report data for relative permeability for high and low tension systems at temperatures ranging from 22°C to 175°C. They state that temperature affects relative permeability especially at low IFTs and describe the effects of temperature at low and high IFTs. They also state that the relative permeability of water and oil will increase with decreasing IFT for constant temperature, while the rate effect is not important after a critical minimum point.

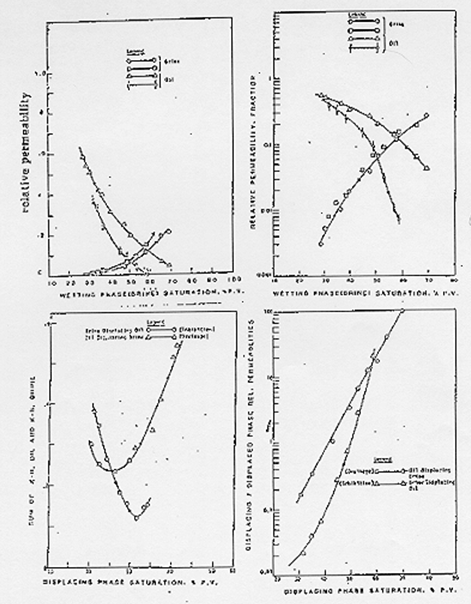
Figure 2-84: Relative Permeability Curves of Berea Sandstone, Strong Water-Wet Conditions (Sankar 1979)

Yadav et al (1984A) (1984B) studied the distribution of two immiscible fluids in the pore space of sandstones. This distribution can give us information about the percentage of each pore that is occupied by each phase and therefore the microscopic information that is necessary for relative permeability studies at the pore level.

Naar and Henderson (1961) correlated relative permeability characteristics during imbibition to the ones from drainage or drainage capillary curves for two-phase flow. A similar work for three-phase flow is given by Naar and Wydal (1961).

Downie and Crane (1961) and Odeh (1959) examined the effect of viscosity on relative permeability. Although their results contradict each other, it is shown that viscosity must be taken into account when the relative permeability values are calculated. However, this value is a property of the medium and it is not a function of the fluid viscosity.

Morgan and Gordon (1970) investigated the effect of pore geometry on water-oil relative permeability. They grouped porous media in categories according to the volume and the interconnectivity of the pores and they provide characteristic curves for each different case.

Morrow and McCaffery (1977) present results of experimental studies of the effect of wettability on relative permeability, capillary pressure and spontaneous imbibition. They classify the uniformly wetted systems in Wetted ( contact angle 0°-62° ), Intermediately-Wetted ( contact angle 62°-133° ) and Non-Wetted ( contact angle 133°-180° ).

Sigmund and McCaffery (1979) introduced a nonlinear least square procedure to analyse the recovery and pressure response to two-phase laboratory displacement tests. They state that two-parameter relative permeability curves determined by a least squares one-dimensional simulation history match could describe quantitatively the dynamic two-phase flow characteristics of various rock types with differing degrees of heterogeneity. They determined the relative permeability characteristics in the form of two saturation exponent parameters. They made simulator calculations and found out that capillary forces significantly affect the pressure and recovery response data obtained from dynamic displacement test. Capillary forces are most likely to have influence on low rate displacements in the drainage direction.

Batycky et al (1981 B) presented a procedure to test the results of the above work. They performed tests in both high-rate displacement and low-rate displacement and they found out that for low-rate displacement there has to be consideration of effects due to capillary forces and the “end-effects”. These effects can extend over significant portions of the core in systems with strong wetting characteristics. They also found that there is high possibility of a significant error in the simulation of relative permeability curves if the capillary forces are neglected.

Thomeer (1983) proposes a relationship to determine air permeability from the mercury/air capillary pressure data. Similar relationships are reported by Swanson (1981) for brine permeability.

Bardon and Longeron (1980) studied the influence of IFTs, flow rates and viscosity ratios on Fontainebleau sandstone. They found out that if the lFT is greater than 0.04 mN/m, the relative permeability can be predicted through a simulation but, for very low IFTs, there are great changes in relative permeability values and the prediction is not satisfactory.

The macroscopic anisotropy and the heterogeneities of a porous medium are a common phenomenon in oil reservoirs. The terms of directional, vertical and horizontal permeabilities appear in many papers that describe the effect of heterogeneity in permeability and reservoir behaviour. Warren and Price (1961), Parsons (1972), Rose (1982), and Aguilera (1982) (for the case of naturally fractured reservoirs), give descriptions and methods on the aspects that govern those systems.

Another area of great interest is the one that deals with low permeability cores. Such cores can be provided from tight gas reservoirs, but the measurements must take into consideration the Klinkenberg effect as well as the effect of confining pressure. There have been quite a few papers in this area although no modeling has been attempted, as far as we know. Reports have been given by Thomas and Ward (1972), Jones and Owens (1980), Walls (1982) (who suggests that a network approach might be the most appropriate modelling approach for this kind of media), Kassemi (1982), Keighin and Sampath (1982) and Freeman and Bush (1983).

Finally, Jones and Roszelle (1978) suggest that some graphical techniques can be used for simple and accurate determination, of relative permeability.