Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Multi-phase Saturated Rock Properties:

Capillary Pressure in Packing Spheres

The relation between the pressure difference across an interface and tension can be determined by displacing the interface an infinitesimal distance in the direction of the normal to the interface. When the system is in mechanical equilibrium, the work to stretch (or contract) the interface is balanced by the pressure – volume work done in displacing the interface. The equation for mechanical equilibrium across a fluid interface is the Young – Laplace equation:

Where

• σ is the surface or interfacial tension
• H is the mean curvature
• Δp is the pressure difference across the interface such that the higher pressure is on the concave side of the interface.

The mean curvature can be expressed as a function of the radius of curvatures:

A general expression of capillary pressure as a function of interfacial tension and curvature of the interface can be generated by substitution of H in eq.(2‑80) into the Young-Laplace eq. (2‑79):

Where R₁ and R₂ are the principle radii of the curvature of the interface that are measured in perpendicular planes and  is the interfacial tension between the fluids.  In the case of a curved interface between immiscible fluids the plus sign is used.  In the case of pendular rings (Figure 2‑46) the minus sign is used.

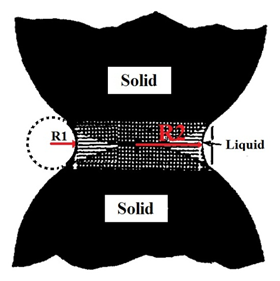
Figure 2-46: Principle Radii for Wetting and Spherical Grain

Comparing eq.(2‑81) with eq.(2‑78) in capillary tube, it is found that the mean radius R_m is defined by

It is impossible to measure the values of R₁ and R₂ , so they are generally referred to by mean radius of the curvature and empirically determined from other measurements on a porous medium.

For a fluid-fluid interface in a capillary tube:

Where ‘r’ is the radius of the capillary and θ is the contact angle.

Wettability determines the fluid distribution in a porous medium. Wetting phase has tendency to occupy the smaller pores. In a packing bed porous medium 2 different types of wetting phase distribution can be found, depend on the saturation of the wetting phase. These two types are funicular distribution and pendular-ring distribution (Figure 2‑47). By decreasing the wetting phase saturation distribution type changes from funicular to pendular. In funicular distribution the wetting phase completely covers the solid surface and is continues through the system. But by decreasing the saturation this continuity is failed and non-wetting phase is contact with some of the solid surface and wetting phase occupies the smaller spaces (pendular distribution).

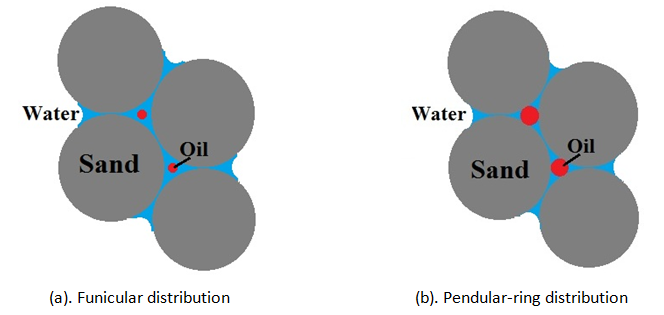
Figure 2-47: Wetting and non-Wetting Fluid Distribution About Inter Grain Contact of Sphere

By decreasing the saturation R₁ and R₂ both tend to decrease in size. According to the eq.(2‑68) capillary pressure increases by decreasing the principle radii. So, capillary pressure can be expressed as a function of rock saturation when the rock is saturated by two immiscible fluids. Also for this specific medium it is possible to find the pore distribution because capillary pressure would be dependent upon the area of the various pores for any particular value of the saturation.