Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
Fluid Properties in Miscible Displacement: Macroscopic Displacement Efficiency
Viscous Fingering
When the mobility ratio between displacing solvent and displaced oil is equal or less than one and the gravity does not influence the displacement by segregating the two fluids, the oil is displaced efficiently ahead of the solvent, and the solvent does not penetrate into the oil except dictated by dispersion. The displacement front is stable. For mobility ratio greater than one the solvent front became unstable and a numerous fingers of solvent develop and penetrate into the oil in an irregular fashion. These viscous fingers result in earlier solvent breakthrough and poorer oil recovery. Figure 5‑33 shows the viscous fingering observed in areal laboratory five spot models for displacement at various mobility ratios.
The severity of the areal fingering increases as mobility ratio becomes more unfavorable, resulting in earlier solvent breakthroughs. The reason for displacement front instability when mobility ratio is unfavorable can be visualized with a simple illustration shown in Figure 5‑34. In this illustration, solvent displaces oil linearly from a porous medium that initially is fully saturated with. The mobility ratio is the ratio of the viscosities and dispersion is assumed negligible. In the absence of heterogeneity the front should be remain a plane surface throughout the displacement. At the time of consideration of the system, the solvent front is located at position xf along the flow path. In the flow region bounded by the dashed lines, a small perturbation or protrusion of the solvent front has occurred such that the front location is at the position xf + ε. The focus of the analysis is the determination of conditions under which e grows in time because if ε does grow in time, the front will be unstable; i.e viscous finger will form along the front. At condition where e does not grow or even diminishes in size, the front stability or uniformity will be maintained. For the normal flat front, pressure drop across the length is given by: Where v is Darcy velocity and Δp is a negative value. The above equation can be solved for interstitial velocity, v, which is equal to the velocity of the front: Where, M is mobility ratio A similar analysis applied to the perturbed area gives: Subtracting eq. () from eq. () resulted: For << xƒ : Therefore: Where t is time. Thus according to eq.(5‑40), grows exponentially with time immediately after formation of the perturbation if M > 1 but decays exponentially with time if M < 1. Dispersion which was not taken into account in this simple example acts to oppose this growth by moderating the viscosity contrast. Whether or not the finger propagate after being initiated and, if so, at what rate depends on the importance of dispersion in the displacement. The initial growth rate can be estimated from the above equation but the equation is not valid for fully developed fingers. Koval[2] developed a model for predicting the performance of miscible displacements in the presence of viscous fingers. He defined an effective viscosity ratio, E, that characterizes the effect of viscous fingering: Koval determined breakthrough volumetric displacement efficiency in homogeneous linear system as a function of E (Figure 5‑35 – Estimated breakthrough recovery as a function of viscosity ratio [??].). Figure 5‑36 shows results from two sets of experiments on a linear system. In the first set, CO2 displaces the oil by FCM process. The viscosity ratio was 16. In the second experiment CO2 displaces oil in a MCM process, while viscosity ratio is 21. There was no mobile water in these experiments. In both experiments the oil recovery was delayed because of the adverse mobility ratio, i.e., there was an early breakthrough of CO2. In FCM process, ultimate recovery approached 100% with continued injection of CO2. In the MCM process the viscous fingering not only delayed the oil recovery but also worked to reduced total recovery. The implication is that an interaction or collaboration occurs between viscous fingering and phase behavior to cause liquid-phase drop out and trapping. [1] “Viscous fingering in five-spot experimental porous media: new experimental results and numerical simulation”, Zhang, H.R., Sorbie, K.S., Teibuklis, N. B., Chemical Enoineerinq Science, Vol. 52, No. I, pp. 37·54, 1997. [3] “An Investigation of Phase Behavior/Microscopic By-Passing Interaction in CO2 Flooding”, Gardner, J.W. and Ypma, J.G.J., SPEJ, Oct.1984. If you have any questions at all, please feel free to ask PERM! We are here to help the community.
Figure 5-33: Displacement Front for a Miscible Displacement Process with Unfavorable Mobility Ratio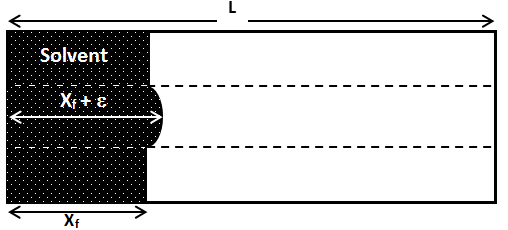
Figure 5-34: Simplified Model of Frontal Instability
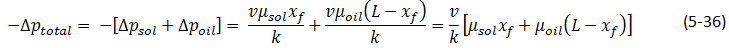
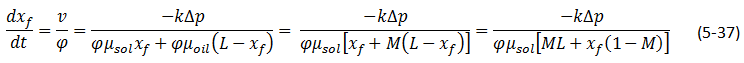
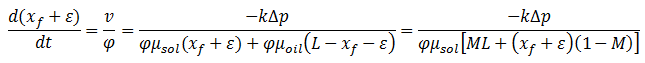
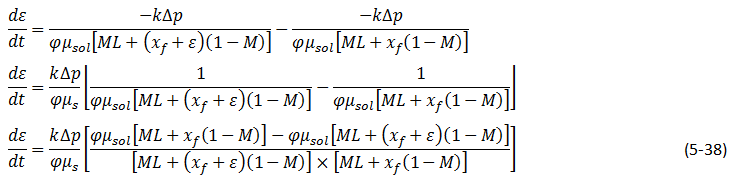



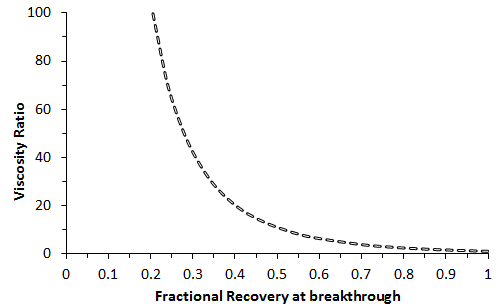
Figure 5-35: Estimated Breakthrough Recovery as a Function of Viscosity Ratio[??]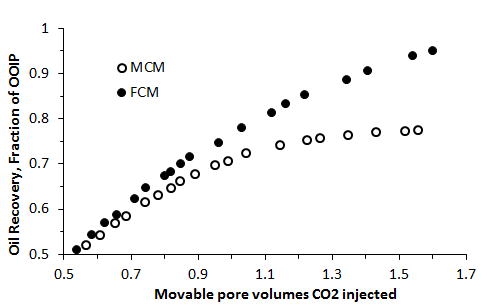
Figure 5-36: Impact of Viscous Instability on Secondary CO2 Flood Oil Recovery Efficiency[3]References
Questions?
