Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
Fluid Properties in Miscible Displacement: Macroscopic Displacement Efficiency
Gravity Effect[29]
From flow experiments in a vertical cross-sectional laboratory model packed with glass beads, Crane et al.[1] found that four flow regimes are possible at unfavorable mobility rations, depending on the value of the dimensionless group characterizing the ratio of viscous and gravity forces (eq. (5‑42)).
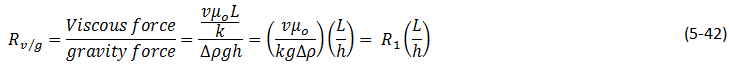
Where g is gravity acceleration.
And for field units:
Where,
v = Darcy velocity, (B/Day/ft2)
L = distance between injection and producing wells (length of the system) ft,
H = height of the reservoir (system), ft,
k = porous medium permeability, md,
μo = oil viscosity, cP,
Δρ = density difference between displacing and displaced fluids, g/cm3.
These equations assume that vertical permeability is the same as horizontal permeability. When this assumption is not true a suggestion approximation is to substitute k with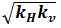 
in this equation.
The magnitude of viscous forces to gravity forces increases with increasing Rv / g value. At small Rv / g values, the displaced phase tends to override (Figure 5‑37.a) or underride (Figure 5‑38.b), depending on the magnitude of the liquids densities, which leads to early breakthrough of the displacing phase, even for M = 1.
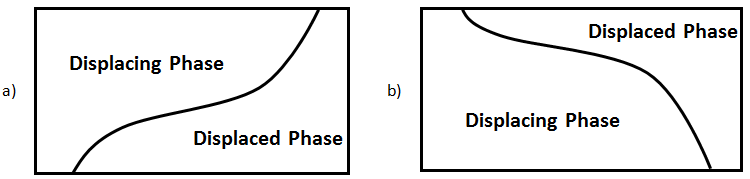
Figure 5-37: Gravity Segregation in Displacement Processes. A) Gravity Override ρo < ρs B) Gravity Underride ρs < ρo
In this manner the displacement is characterized by a single gravity tongue (Figure 5‑38, a, Regime I). The geometry of this tongue and vertical sweepout both depend on the particular Rv / g of the displacement. At higher value of Rv / g the displacement is still characterized by a single gravity tongue (Figure 5‑38, a, Regime II), but vertical sweepout become independent of the particular value of Rv / g until a critical value is exceeded. Beyond this critical value a transition region is encountered (Figure 5‑38, b, Regime III) where viscous fingers are formed along the primary gravity tongue. Vertical sweep is improved by the formation of viscous fingers in this regime. In this regime, sweep out for a given value of pore volumes injected increases sharply with increasing values of Rv / g. Finally, a value of Rv / g is reached where the displacement is entirely dominated by multiple fingering in the cross section and vertical sweepout again becomes independent of the particular value of the Rv / g (Figure 5‑38, c, Regime IV). A gravity tongue does not form in this regime because of the strong viscous fingering. The value of Rv / g at which a transition occurs from one flow regime to another depends on the mobility ratio.
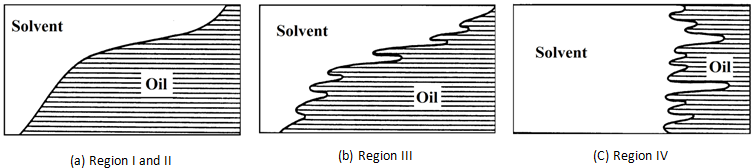
Figure 5-38: Flow Regimes for Miscible Displacement in a Vertical Cross Section
Figure 5‑39 further illustrate the different flow regimes in miscible displacement and shows how sweepout at solvent breakthrough in a vertical cross section is affected both by the flow regime and by mobility ratio.
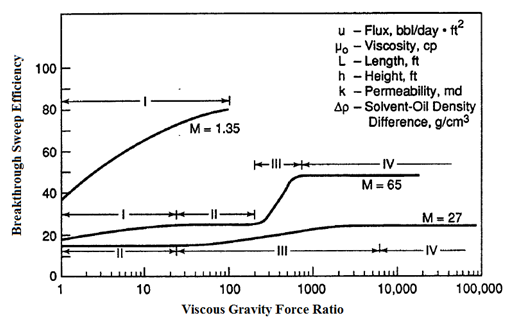
Figure 5-39: Flow Regimes in a Two-Dimensional, Uniform Linear System (Schematic)[29]
Figure 5‑40 shows a relation between mobility ratio, Rv / g and vertical sweep efficiency.
Example 5‑6
A miscible displacement process will be used to displace oil from a linear reservoir having the following properties:
L = 300 ft, h = 10 ft, φ = 0.20, ko = 200 md.
Determining the effect of gravity segregation on the vertical sweep efficiency if the oil is displaced miscibly by a solvent with a density of 0.7 gr/cm3 and a viscosity of 2.3 cp at reservoir temperature. The density of the oil is 0.85 g/cm3 and the viscosity is 2.3 cp. Darcy velocity is 0.075 ft/D.
Solution
Calculate viscous/gravity ratio using eq.(5‑43):
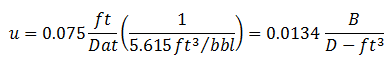
And
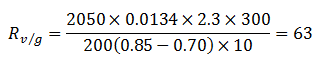
Calculate M:
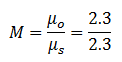
From Figure 5‑40 vertical displacement efficiency (EI) at breakthrough is 0.86.
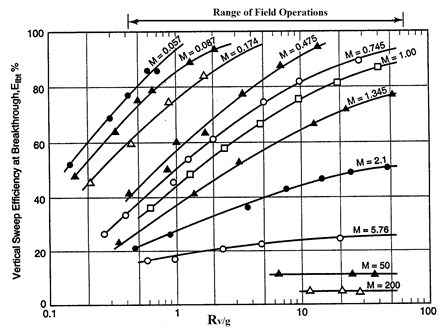
Figure 5-40: Volumetric Sweep Efficiency at Brekathrough as a Function of the Viscous / Gravity Force Ratio[2]
References
[2] “A laboratory study of gravity segregation in frontal drives”, Craig, F.F. Jr. et al., Trans, AIME (1957) 210, 275-82.
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
From flow experiments in a vertical cross-sectional laboratory model packed with glass beads, Crane et al.[1] found that four flow regimes are possible at unfavorable mobility rations, depending on the value of the dimensionless group characterizing the ratio of viscous and gravity forces (eq. (5‑42)).
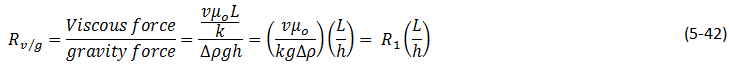
Where g is gravity acceleration.
And for field units:
Where,
v = Darcy velocity, (B/Day/ft2)
L = distance between injection and producing wells (length of the system) ft,
H = height of the reservoir (system), ft,
k = porous medium permeability, md,
μo = oil viscosity, cP,
Δρ = density difference between displacing and displaced fluids, g/cm3.
These equations assume that vertical permeability is the same as horizontal permeability. When this assumption is not true a suggestion approximation is to substitute k with 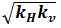in this equation.
The magnitude of viscous forces to gravity forces increases with increasing Rv / g value. At small Rv / g values, the displaced phase tends to override (Figure 5‑37.a) or underride (Figure 5‑38.b), depending on the magnitude of the liquids densities, which leads to early breakthrough of the displacing phase, even for M = 1.
Figure 5-37: Gravity Segregation in Displacement Processes. A) Gravity Override ρo < ρs B) Gravity Underride ρs < ρo
In this manner the displacement is characterized by a single gravity tongue (Figure 5‑38, a, Regime I). The geometry of this tongue and vertical sweepout both depend on the particular Rv / g of the displacement. At higher value of Rv / g the displacement is still characterized by a single gravity tongue (Figure 5‑38, a, Regime II), but vertical sweepout become independent of the particular value of Rv / g until a critical value is exceeded. Beyond this critical value a transition region is encountered (Figure 5‑38, b, Regime III) where viscous fingers are formed along the primary gravity tongue. Vertical sweep is improved by the formation of viscous fingers in this regime. In this regime, sweep out for a given value of pore volumes injected increases sharply with increasing values of Rv / g. Finally, a value of Rv / g is reached where the displacement is entirely dominated by multiple fingering in the cross section and vertical sweepout again becomes independent of the particular value of the Rv / g (Figure 5‑38, c, Regime IV). A gravity tongue does not form in this regime because of the strong viscous fingering. The value of Rv / g at which a transition occurs from one flow regime to another depends on the mobility ratio.
Figure 5-38: Flow Regimes for Miscible Displacement in a Vertical Cross Section
Figure 5‑39 further illustrate the different flow regimes in miscible displacement and shows how sweepout at solvent breakthrough in a vertical cross section is affected both by the flow regime and by mobility ratio.
Figure 5-39: Flow Regimes in a Two-Dimensional, Uniform Linear System (Schematic)[29]
Figure 5‑40 shows a relation between mobility ratio, Rv / g and vertical sweep efficiency.
Example 5‑6
A miscible displacement process will be used to displace oil from a linear reservoir having the following properties:
L = 300 ft, h = 10 ft, φ = 0.20, ko = 200 md.
Determining the effect of gravity segregation on the vertical sweep efficiency if the oil is displaced miscibly by a solvent with a density of 0.7 gr/cm3 and a viscosity of 2.3 cp at reservoir temperature. The density of the oil is 0.85 g/cm3 and the viscosity is 2.3 cp. Darcy velocity is 0.075 ft/D.
Solution
Calculate viscous/gravity ratio using eq.(5‑43):
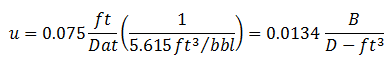
And
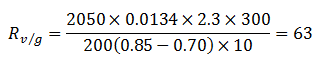
Calculate M:
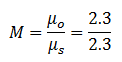
From Figure 5‑40 vertical displacement efficiency (EI) at breakthrough is 0.86.
Figure 5-40: Volumetric Sweep Efficiency at Brekathrough as a Function of the Viscous / Gravity Force Ratio[2]
References
[2] “A laboratory study of gravity segregation in frontal drives”, Craig, F.F. Jr. et al., Trans, AIME (1957) 210, 275-82.
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.