Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
Fluid Properties in Miscible Displacement: Fluid Viscosity
Mobility ratio in a displacement process is a direct function of the viscosities of displaced and displacing fluids. For miscible displacements, assuming the relative permeability relationships of the different non aqueous fluids are the same so:

Where,
M = Mobility ratio,
KrD = Displacing relative permeability,
Krd = Displaced relative permeability,
μD = Displacing fluid viscosity,
μd = Displaced fluid viscosity.
So Knowledge of oil viscosity is vital to the petroleum industry, and is especially important when considering production of heavy oil and bitumen. Knowledge of oil viscosity is vital to the petroleum industry, and is especially important when considering production of heavy oil and bitumen and other EOR methods. Viscosity can determine the success or failure of a given EOR scheme and it is an important parameter for doing numerical simulation and determining the economics of a project.
Viscosity is a function of pressure, temperature and composition. The viscosities of crude oils vary over a wide range. There are some correlations for prediction of liquids and gases viscosity based on the fluid composition. The following equations are the most well-known correlations for prediction of viscosity.
Lorentz-Bray-Clark Method[1]
The procedure of this method for reservoir liquids was developed using the residual viscosity concept and theory of corresponding states. It was the first known procedure for calculating the viscosity of reservoir liquids from their compositions.
Jossi et al.[2], developed the following equation for viscosity of the pure liquid components:
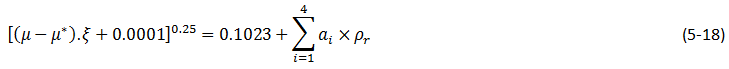
Where,
a1 = 0.023364
a2 = 0.058533
a3 = -0.40758
a4 = 0.0093324
μ* = Viscosity at normal pressure,
ζ = Viscosity parameter:

ρr = Reduced molar density:

M = Molecular Weight,
TC = Critical temperature,
PC = Critical pressure
ρC = Critical molar density.
Hering and Zipper[3] introduced the following equation for μ* of a mixture (liquid or gas):

To find the viscosity of a liquid mixture Lorentz et al. used eq. (5‑18) with μ* and ζ value for mixture. They used eq. (5‑21) to find the μ* for mixture and defined ζ of a liquid mixture as functions of the composition Xi , the component molecular weights, critical pressure and critical temperatures:
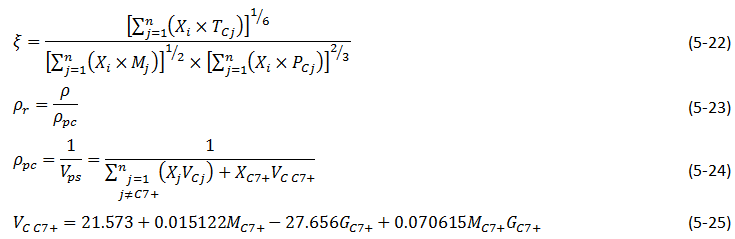
Where,
ρpc = pseudocritical density of the multi component liquid,
Vpc = pseudocritical volume for the mixture,
VCj = critical volume of component j,
GC7+ = Specific gravity of C7+ fraction of the oil.
The Modified Lorentz-Bray-Clark Method
A modified form of the Lorentz-Bray-Clark method can also be used:
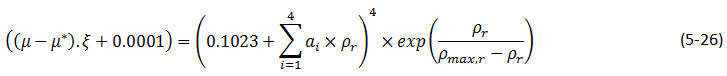
This modified equation is intended to improve the modeling of the behavior of heavy oils. In this equation the viscosity increases exponentially as the reduced molar density ρr approaches a maximum ρmax, r for small values of ρr , ρmax, r >> ρr , the modified Lorentz-Bray-Clark methodhas the same form as eq. (5‑18).
The Pederson Method[4]
It is a corresponding states compositional viscosity model that enables viscosity prediction for black oil systems using compositional data.
The prediction of viscosity according to the oil composition, is crucial for compositional simulation of the miscible process because of composition change of the displaced and displacing fluid. There are several experimental type methods that can measure the viscosity of the fluids. From the wide range of experimental tools for viscosity measurement, NMR is explained in the following subsection.
Measuring Viscosity Using NMR
As viscosity increases, conventional measurements become progressively less accurate and more difficult to obtain. Oil viscosities measured in the lab may also be not indicative of true in-situ viscosities. An alternate method is required for predicting oil viscosity, especially if this method can be applied in-situ. Low field nuclear magnetic resonance (NMR) is an attractive alternative to conventional viscosity measurements, as its measurements are fast, non-destructive and insensitive to technician error.
Bryan and Kantzas did an extensive work on the application of NMR in determination of heavy oil and bitumen viscosity as well as crude oil emulsion. Their work lead to some correlations that predict viscosities from less than 1 cP to over 3,000,000 cP over 25-80°C based on the NMR data[5]. Bryan et. al.[5] provided a detailed explanation viscosity that is helpful to understand the basics that make NMR as a powerful tool in viscosity determination:
Newtonian fluids exhibit a linear relationship between shear stress and shear rate, given by Newton’s law of viscosity:

Where,
τ = Shear stress (Pa),
μ = Viscosity,
γ = Shear rate (s-1).
For a Newtonian fluid at a constant temperature and pressure, viscosity is a constant value. If the fluid is non-Newtonian, however, viscosity changes with shear rate. Most crude oil emulsions that contain low to moderate dispersed water are Newtonian, but non-Newtonian effects may be observed at higher dispersed water fractions. Eyring’s theory of viscosity states that the empty space between the closely packed molecules in a liquid is not enough for the molecules to move freely by one another. In order for a molecule to move, therefore, other surrounding molecules must first give way and create a space or “hole” for this molecule to enter, eq. (5‑28). Highly viscous fluids have molecules that are complex and close together, so it is difficult for their molecules to move enough to create this space. Not all molecules have enough energy to overcome the attractive forces of their neighbors enough to move, so the concentration of activated molecules that are able to move is therefore related to the viscosity of the fluid.

Where,
δ = Distance between molecular layers in a fluid,
A = Distance between a molecule and an adjacent empty lattice site,
N = Avogadro number,
h = Planck constant,
V = liquid molar volume,
ΔG0 = free energy of act
As temperature increases, more the molecules have enough energy to breach this activation energy barrier and are able to move by one another more easily. At higher temperatures the spaces between the molecules are also likely to be larger, so the free energy of the molecules required for flow will also be less. This leads to lower viscosity at elevated temperatures. The development of Eq. (5-28) allows for a qualitative understanding of what causes differences in viscosity between fluids and for viscosity to be estimated on the basis of the molecular properties of the liquid.
Low-field NMR measures the response of hydrogen protons in external magnetic fields. Protons are present in oil and water and have a strong relaxation response to imposed magnetic signal pulses. In the presence of magnetic field the protons will line up either parallel or anti-parallel to the field lines. A pulse sequence is then applied to these protons to tip them 90° onto the transverse plane. As the protons give off energy, they return to their equilibrium position. A low field NMR experiment can therefore provide two pieces of information: the strength of the signal from the protons and a characteristic relaxation time. This characteristic relaxation time is either the time for the signal to reappear in the longitudinal equilibrium plane (T1), or the time for the signal to disappear in the transverse plane (T2), (for more details return to chapter 3). T2 measurements are used in viscosity measurements[6]. The pulse sequence applied to the protons gives them energy and tips them into the transverse plane. In order to return to their equilibrium direction, these excited protons must give off their energy. Once they do so, the signal in the transverse plane decays and relaxation is said to have occurred. In the experiments for viscosity measurements two types of relaxation occur in porous media:
- Bulk relaxation (T2B),
- Surface relaxation (T2S).
Bulk relaxation is a fluid property, and is a measure of how easily the protons give off energy to one another. Bulk relaxation can be therefore expressed in the following form[7]:

Where, T is absolute temperature of the sample. According to eq. (5‑29) the bulk relaxation rate is directly proportional to the fluid viscosity, so viscous fluids will have faster relaxation rates than fluids with lower viscosity. The reason for this is that the protons must give off their energy to other protons before they can return to their equilibrium direction. Samples with higher viscosities have molecules that cannot move past one another as easily. The protons of these fluids will therefore contact one another at a higher frequency, leading to energy being given off faster.
When fluids are in constricted spaces like pores, energy can also be transferred from the proton spins to the pore walls. This is termed surface relaxation, and is given by:

Where,
ρ = The surface relaxivity of the pore wall,
V = Pore Volume,
S = Pore Surface.
From eq. (5‑30) it can be seen that fluid found in smaller pores (where v / s is smaller) will tend to relax faster, and T2S will be smaller. Bryan et al. used 112 oil samples with viscosity range of around 1 to 3,000,000 cP to develop the model based on the NMR data the oil samples with known viscosity values has been tested with NMR to find the NMR parameters for each sample using linear regresion. The following equation was developed that can be used to predict the viscosity of an oil sample using the NMR parameters:

Where,
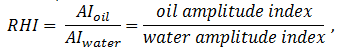
T2gm_oil = the geometric mean T2 value (ms).
References
[1] “Calculating Viscosity of Reservoir Fluids from their Composition”, Lorentz, J., Bray, B. G. and Clark, C. R. J., Journal of Petrolleum Technology 1171, p. 231, 1964
[2] “The Viscosity of Pure Substances in the Dense Gaseous and Liquid Phases”, Jossi, J. A., Stiel, L. I., Thodos G., AIChE journal. (1962) 8, 59
[3] “Calculation of viscosity of technical gas mixtures from the viscosity of individual gases”, Herning, F. and Zipper, L., Gas u. Wasserfach (1936) 79, No. 49, 69
[4] “Properties of Oils and Natural Gases”, Pederson, K. S., Fredenslund, A. and Thomassen, P., Contribution in Petroleum Geology and Engineering Vol. 5, Gulf, Houston, 1989
[5] “Viscosity Predictions for Crude Oils and Crude Oil Emulsions Using Low Field NMR”, Bryan, J., Kantzas, A., Bellehumeur, C., SPE No. 77329, 2002.
[6] “Oil-Viscosity Predictions from Low-Field NMR Measurements”, Bryan, J., Kantzas, A., Bellehumeur, C., SPE No. 89070, 2005
[7] “In Situ Viscosity of Oil Sands Using Low Field NMR”, Bryan, J., Kantzas, A., Moon, D., Petroleum Society’s Canadian International Petroleum Conference, 2003
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
The procedure of this method for reservoir liquids was developed using the residual viscosity concept and theory of corresponding states. It was the first known procedure for calculating the viscosity of reservoir liquids from their compositions.
Jossi et al.[2], developed the following equation for viscosity of the pure liquid components:
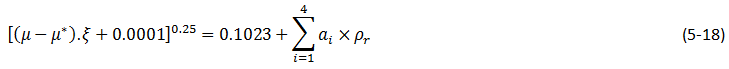
Where,
μ* = Viscosity at normal pressure,
ζ = Viscosity parameter:

ρr = Reduced molar density:

M = Molecular Weight,
TC = Critical temperature,
PC = Critical pressure
ρC = Critical molar density.
Hering and Zipper[3] introduced the following equation for μ* of a mixture (liquid or gas):

To find the viscosity of a liquid mixture Lorentz et al. used eq. (5‑18) with μ* and ζ value for mixture. They used eq. (5‑21) to find the μ* for mixture and defined ζ of a liquid mixture as functions of the composition Xi , the component molecular weights, critical pressure and critical temperatures:
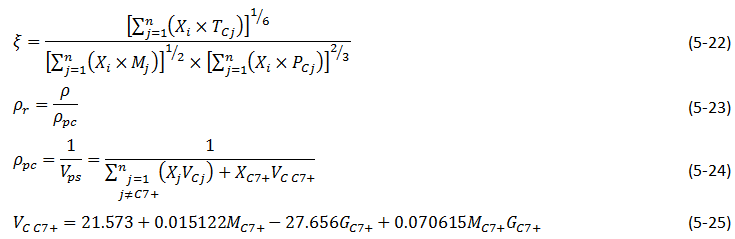
Where,
ρpc = pseudocritical density of the multi component liquid,
Vpc = pseudocritical volume for the mixture,
VCj = critical volume of component j,
GC7+ = Specific gravity of C7+ fraction of the oil.
The Modified Lorentz-Bray-Clark Method
A modified form of the Lorentz-Bray-Clark method can also be used:
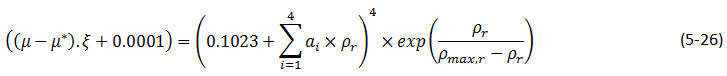
This modified equation is intended to improve the modeling of the behavior of heavy oils. In this equation the viscosity increases exponentially as the reduced molar density ρr approaches a maximum ρmax, r for small values of ρr , ρmax, r >> ρr , the modified Lorentz-Bray-Clark methodhas the same form as eq. (5‑18).
The Pederson Method[4]
It is a corresponding states compositional viscosity model that enables viscosity prediction for black oil systems using compositional data.
The prediction of viscosity according to the oil composition, is crucial for compositional simulation of the miscible process because of composition change of the displaced and displacing fluid. There are several experimental type methods that can measure the viscosity of the fluids. From the wide range of experimental tools for viscosity measurement, NMR is explained in the following subsection.
Measuring Viscosity Using NMR
As viscosity increases, conventional measurements become progressively less accurate and more difficult to obtain. Oil viscosities measured in the lab may also be not indicative of true in-situ viscosities. An alternate method is required for predicting oil viscosity, especially if this method can be applied in-situ. Low field nuclear magnetic resonance (NMR) is an attractive alternative to conventional viscosity measurements, as its measurements are fast, non-destructive and insensitive to technician error.
Bryan and Kantzas did an extensive work on the application of NMR in determination of heavy oil and bitumen viscosity as well as crude oil emulsion. Their work lead to some correlations that predict viscosities from less than 1 cP to over 3,000,000 cP over 25-80°C based on the NMR data[5]. Bryan et. al.[5] provided a detailed explanation viscosity that is helpful to understand the basics that make NMR as a powerful tool in viscosity determination:
Newtonian fluids exhibit a linear relationship between shear stress and shear rate, given by Newton’s law of viscosity:

Where,
τ = Shear stress (Pa),
μ = Viscosity,
γ = Shear rate (s-1).
For a Newtonian fluid at a constant temperature and pressure, viscosity is a constant value. If the fluid is non-Newtonian, however, viscosity changes with shear rate. Most crude oil emulsions that contain low to moderate dispersed water are Newtonian, but non-Newtonian effects may be observed at higher dispersed water fractions. Eyring’s theory of viscosity states that the empty space between the closely packed molecules in a liquid is not enough for the molecules to move freely by one another. In order for a molecule to move, therefore, other surrounding molecules must first give way and create a space or “hole” for this molecule to enter, eq. (5‑28). Highly viscous fluids have molecules that are complex and close together, so it is difficult for their molecules to move enough to create this space. Not all molecules have enough energy to overcome the attractive forces of their neighbors enough to move, so the concentration of activated molecules that are able to move is therefore related to the viscosity of the fluid.

Where,
δ = Distance between molecular layers in a fluid,
A = Distance between a molecule and an adjacent empty lattice site,
N = Avogadro number,
h = Planck constant,
V = liquid molar volume,
ΔG0 = free energy of act
As temperature increases, more the molecules have enough energy to breach this activation energy barrier and are able to move by one another more easily. At higher temperatures the spaces between the molecules are also likely to be larger, so the free energy of the molecules required for flow will also be less. This leads to lower viscosity at elevated temperatures. The development of Eq. (5-28) allows for a qualitative understanding of what causes differences in viscosity between fluids and for viscosity to be estimated on the basis of the molecular properties of the liquid.
Low-field NMR measures the response of hydrogen protons in external magnetic fields. Protons are present in oil and water and have a strong relaxation response to imposed magnetic signal pulses. In the presence of magnetic field the protons will line up either parallel or anti-parallel to the field lines. A pulse sequence is then applied to these protons to tip them 90° onto the transverse plane. As the protons give off energy, they return to their equilibrium position. A low field NMR experiment can therefore provide two pieces of information: the strength of the signal from the protons and a characteristic relaxation time. This characteristic relaxation time is either the time for the signal to reappear in the longitudinal equilibrium plane (T1), or the time for the signal to disappear in the transverse plane (T2), (for more details return to chapter 3). T2 measurements are used in viscosity measurements[6]. The pulse sequence applied to the protons gives them energy and tips them into the transverse plane. In order to return to their equilibrium direction, these excited protons must give off their energy. Once they do so, the signal in the transverse plane decays and relaxation is said to have occurred. In the experiments for viscosity measurements two types of relaxation occur in porous media:
- Bulk relaxation (T2B),
- Surface relaxation (T2S).
Bulk relaxation is a fluid property, and is a measure of how easily the protons give off energy to one another. Bulk relaxation can be therefore expressed in the following form[7]:

Where, T is absolute temperature of the sample. According to eq. (5‑29) the bulk relaxation rate is directly proportional to the fluid viscosity, so viscous fluids will have faster relaxation rates than fluids with lower viscosity. The reason for this is that the protons must give off their energy to other protons before they can return to their equilibrium direction. Samples with higher viscosities have molecules that cannot move past one another as easily. The protons of these fluids will therefore contact one another at a higher frequency, leading to energy being given off faster.
When fluids are in constricted spaces like pores, energy can also be transferred from the proton spins to the pore walls. This is termed surface relaxation, and is given by:

Where,
ρ = The surface relaxivity of the pore wall,
V = Pore Volume,
S = Pore Surface.
From eq. (5‑30) it can be seen that fluid found in smaller pores (where v / s is smaller) will tend to relax faster, and T2S will be smaller. Bryan et al. used 112 oil samples with viscosity range of around 1 to 3,000,000 cP to develop the model based on the NMR data the oil samples with known viscosity values has been tested with NMR to find the NMR parameters for each sample using linear regresion. The following equation was developed that can be used to predict the viscosity of an oil sample using the NMR parameters:

Where,
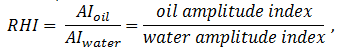
T2gm_oil = the geometric mean T2 value (ms).
References
[1] “Calculating Viscosity of Reservoir Fluids from their Composition”, Lorentz, J., Bray, B. G. and Clark, C. R. J., Journal of Petrolleum Technology 1171, p. 231, 1964
[2] “The Viscosity of Pure Substances in the Dense Gaseous and Liquid Phases”, Jossi, J. A., Stiel, L. I., Thodos G., AIChE journal. (1962) 8, 59
[3] “Calculation of viscosity of technical gas mixtures from the viscosity of individual gases”, Herning, F. and Zipper, L., Gas u. Wasserfach (1936) 79, No. 49, 69
[4] “Properties of Oils and Natural Gases”, Pederson, K. S., Fredenslund, A. and Thomassen, P., Contribution in Petroleum Geology and Engineering Vol. 5, Gulf, Houston, 1989
[5] “Viscosity Predictions for Crude Oils and Crude Oil Emulsions Using Low Field NMR”, Bryan, J., Kantzas, A., Bellehumeur, C., SPE No. 77329, 2002.
[6] “Oil-Viscosity Predictions from Low-Field NMR Measurements”, Bryan, J., Kantzas, A., Bellehumeur, C., SPE No. 89070, 2005
[7] “In Situ Viscosity of Oil Sands Using Low Field NMR”, Bryan, J., Kantzas, A., Moon, D., Petroleum Society’s Canadian International Petroleum Conference, 2003
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
