Fundamentals of Fluid Flow in Porous Media
Chapter 5
Miscible Displacement
The Equation of Continuity in Porous Media: Solutions to the One-Dimensional Convection-Dispersion Model
The Capacitance Model
Tracer effluent profiles from porous media are often characterized by tailing or deviation from the symmetrical S-shape given by solutions to the convection-dispersion equation at high Peclet number. As a result, a probability plot of these tracer concentrations is concave upward at the high concentration end (Figure 5‑63). As mentioned before this behavior has been attributed to dead-end pores, stagnant regions of pore space not contributing to flow, or partially saturated porous media. It has frequently been modeled by dividing the pore space into a flowing and a stagnant fraction, with some resistance to mass transfer between them. The concept of capacitance is obviously an oversimplification, but provides a convenient tool to model regions of large velocity contrast. The consequence of finite-rate mass transfer between the flowing and stagnant fractions is an increase in the length of the mixing zone.
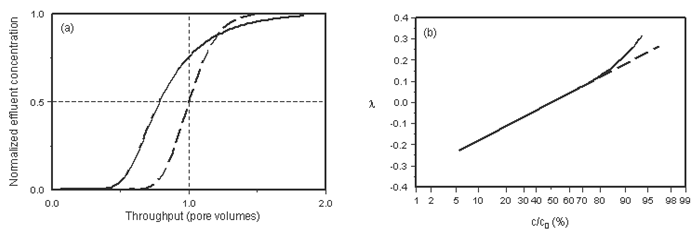
Figure 5-63: The Effects of Capacitance: (a) Illustration of Symmetrical and Skewed Effluent Profiles, (b) Deviation of Probability Plot from Linearity Due to Asymmetry in Effluent Profile
In the presence of capacitance, the one-dimensional convection-dispersion equation becomes

where f is the flowing fraction of the pore volume, and c* is the average concentration in the stagnant fraction. An additional equation specifying the mode of mass transfer between the flowing and stagnant fractions is required. Various models have been used, one of the most common ones being the first order mass transfer model of Coats and Smith (1964):

where c* is assumed to be uniformly mixed, and K is the mass transfer coefficient. Coats and Smith’s model extends a mixing cell capacitance model developed by Deans (1963).
Using the dimensionless variables in eqs (5‑74) and 5‑75), and

Eqs (5‑89) and (5‑90) can be put into non-dimensional form:
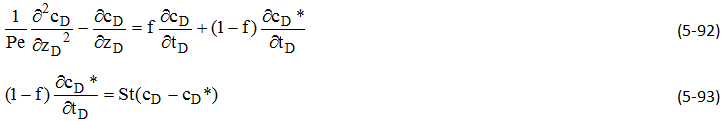
Where, St is the Stanton or Damköhler number, defined by:

Any of the initial and boundary conditions previously discussed can be used with the capacitance model. An initial condition for c* is also required. As well, the discussion of flowing and in-situ concentrations in a previous section applies to the capacitance model (Brigham, 1974; Baker, 1977).
The capacitance model has frequently been solved by numerical techniques, but analytical solutions are also available. When mass transfer is slow, solutions of the capacitance model revert to those for the convection-dispersion equation, with tD replaced by tD / f. Some analytical solutions to the capacitance model and discussions of boundary conditions can be found in papers by Coats and Smith (1964), Bennett and Goodridge (1970), Brigham (1974), de Smedt and Wierenga (1979a,b), and Patel and Greaves (1987).
Questions?
If you have any questions at all, please feel free to ask PERM! We are here to help the community.
