Fundamentals of Fluid Flow in Porous Media

 

Chapter 5

Miscible Displacement

The Equation of Continuity in Porous Media: Equation of Dispersion in Porous Media

Flow in porous media is different from flow in simple capillaries in that a major contribution to mechanical dispersion arises from the complex geometry of the flow paths. Dispersion in porous media results from the same mechanisms that are active in capillaries (molecular diffusion and velocity profiles across the flow channels). However, as mentioned before, additional mechanisms arise from the fact that flow takes place in capillaries that have non-uniform, variable cross-sections and different conductivities. The capillaries run at various angles to the net direction of flow, and mixing and re-splitting of streams takes place at pore junctions. A component of dispersion thus arises from the existence of the porous medium itself.

In general, the dispersion coefficient in porous media is a second-order tensor that depends on local variations of the velocity field and on porous medium characteristics (Bear, 1972). The dependence of dispersion on these quantities cannot be measured easily, and the dispersion coefficient is therefore commonly reduced to a longitudinal component parallel to the net direction of flow, and a transverse component perpendicular to the net direction of flow. Experimentally, it is observed that longitudinal dispersion is larger than transverse dispersion (Blackwell, 1962; Fried and Combarnous, 1971). Dispersion is thus anisotropic.

Theories attempting to model dispersion in porous media have included capillary tube and mixing cell models, networks of fixed and random capillaries, and models that use special averaging and the macroscopic equation of continuity (Fried and Combarnous, 1971; Bear, 1972). Exact mathematical models have been developed only for very simple geometries, such as single capillaries or bundles of capillaries, and for arrays of mixing cells. While capillary models cannot adequately represent porous media, they are useful from a conceptual point of view.

The theory of random walk has often been applied to dispersion modeling. The basic postulate in this approach is that, although it is impossible to predict the exact path of an individual tracer particle, the rules of statistics may be applied to predict the overall behavior of a cloud of tracer particles. The statistical approach has been applied to fixed and random capillary patterns representing simple porous media. A criticism of these geometrical models has been that they are restrictive through the choice of a specific geometrical pattern.

The macroscopic convection-dispersion equation (Equations 6 and 7), which treats the porous medium as a continuum and uses a “lumped” dispersion parameter, has been used most commonly to model dispersion in practice. However, even this, perhaps most general, approach is still closely linked to experiment for estimation of the model parameters.

The dispersion coefficient in porous media is a function of the fluid velocity. Mathematical models for flow in porous media have yielded velocity exponents of either 1 or 2 (Collins, 1961; Fried and Combarnous, 1971; Bear, 1972). Bear (1972) has pointed out that models which consider the combined effects of a velocity distribution across the flow channels and molecular diffusion predict a dispersion coefficient proportional to v2, as in the case of capillary tubes (see Equation 10). Models that take into account only the mean motion of the fluid in the flow channels and assume that complete mixing takes place at their junctions (perfect mixers) lead to a linear relationship between D and v. It has been observed experimentally that the velocity exponent of the dispersion coefficient in porous media is often close to 1.2 (Collins, 1961; Brigham et al., 1961; Bear, 1972).

A general equation that expresses the dependence of dispersion in porous media on velocity can be written as follows (Perkins and Johnston, 1963; Fried and Combarnous, 1971):

Where,

K = porous medium dispersion coefficient,

D_app = apparent molecular diffusion coefficient in the porous medium,

δ = a constant,

σ = a measure of the inhomogeneity of the porous medium,

v = apparent linear velocity,

d_p = average particle diameter,

m = exponent that depends on the flow regime.

The dimensionless quantity dp_p / D_o is the particle Peclet number of molecular diffusion. It expresses the ratio of convective to diffusive mixing, with the particle size as characteristic length. Porous media are generally too complex for exact mathematical description, necessitating the parameters δ and σ.

Eq. (5‑65) shows that dispersion in porous media can be modeled as a sum of diffusive and convective terms, as in the case of capillaries (Eq. (5‑62)). Eq. (5‑65) is often represented graphically in the form of a log-log plot of dimensionless dispersion (D/D₀) versus particle Peclet number ( dp_p / D_o ), or modified particle Peclet number ( avd_p / D_o ). A typical example is shown in Figure 3, from which the following flow regimes can be identified (Perkins and Johnston, 1963).

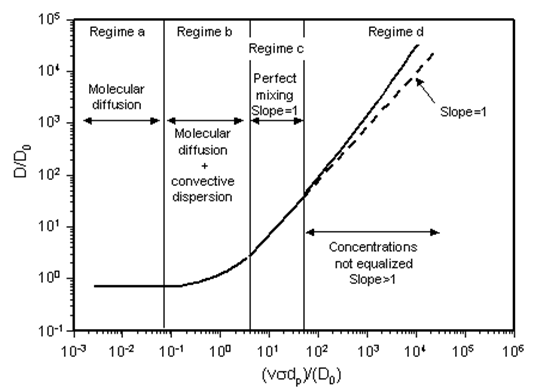
Figure 5-55: Dependence of Dispersion Coefficient on Peclet Number in Different Flow Regimes. The Scales on the Axes Depend on Porous Medium and Other Factors. The Curve SHown Approximates Longitudinal Dispersion in Unconsolidated Random Packs (After Perkins and Johnston, 1963)

Regime a: At low velocities or high molecular diffusion coefficients, molecular diffusion dominates dispersion. The second term in Eq. (5‑65) can be neglected, and the dispersion coefficient is constant and equal to the apparent molecular diffusion coefficient (D_app), which is lower than the true molecular diffusion coefficient because of porous medium tortuosity.

Regime b: The effect of mechanical dispersion becomes significant, and both molecular diffusion and convection contribute to dispersion.

Regime c: In this regime, the porous medium can be modeled as a perfect mixer, and m = 1. This flow regime applies to longitudinal dispersion in random packs when ( 4 < σvd_p / D_o < 50 ) , and to transverse dispersion in similar packs when 100 < σvd_p / D_o < 10⁴ (Perkins and Johnston, 1963).

Regime d: When the Peclet number becomes very high, the concentration in each mixing cell cannot be equalized, and m becomes greater than unity. The exponent m has been found to increase from 1 to approximately 1.25 in this flow regime.

In regimes c and d, molecular diffusion is often neglected, and for practical purposes an equation of the form D = λv , λ being a constant, is used (Fried and Combarnous, 1971; Bear, 1972; van Genuchten and Wierenga, 1977; Satter et al., 1980).

The flow regimes described by different authors are not always consistent. The above description follows that of Perkins and Johnston (1963). Fried and Combarnous (1971) and Bear (1972) have used m = 1 to 1.2 in Regime c and m = 1 in Regime d, and have identified a fifth flow regime for longitudinal dispersion at very high Peclet numbers. In this fifth regime the effects of turbulence become appreciable and Darcy’s law no longer applies. Turbulence causes increased transverse mixing, which reduces longitudinal dispersion; the slope of the curve thus tends to become less than unity.

In a porous medium, there is no sharp transition from laminar to turbulent flow. Defining the particle Reynolds number (Re) in packs of spheres as

Where,

ρ = fluid density,

μ = fluid viscosity.

Laminar flow has been observed at Reynolds numbers lower than 10, while turbulence is fully developed at Reynolds numbers greater than 1000 (Perkins and Johnston, 1963). In the turbulent region, dispersion is often expressed as a particle Peclet number (Pe) of dispersion:

In fully developed turbulent flow, the longitudinal Peclet number approaches 2, and the transverse Peclet number approaches 11 with increasing Reynolds number, Figure 4 (Aris and Amundson, 1957; Perkins and Johnston, 1963).

Turbulent flow is not likely to be encountered in a petroleum reservoir. In a typical reservoir rock we may have:

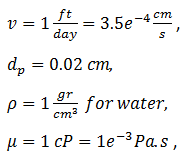
Then:

Re = 7e^-4

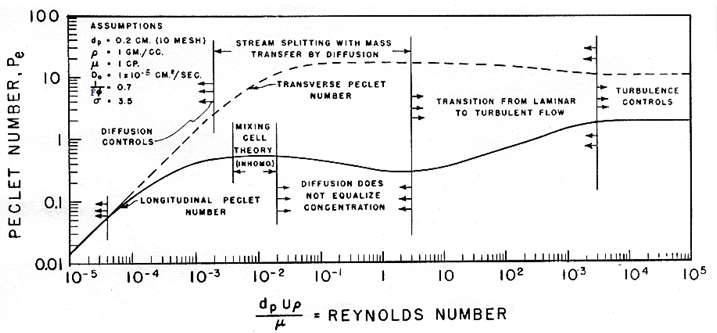
Figure 5-56: Dependence of Peclet Number on Reynolds Number for an Aqueous System (From Perkins and Johnston, 1963)

The general form of eq. (5‑65) and the shape of the curve in Figure 5‑55 apply to longitudinal and transverse dispersion and to different types of porous media, but the transition between flow regimes and the magnitude of the dispersion coefficient are system dependent. Figure 5‑56 is a typical example for longitudinal dispersion in unconsolidated random packs. Blackwell (1962) has given a set of empirical curves that allow estimation of transverse and longitudinal dispersion coefficients in sandpacks (Figure 5‑57).

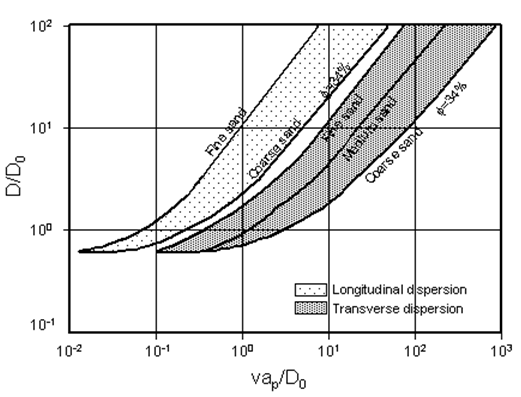
Figure 5-57: Range of Dispersion Coefficients for Various Sandpacks. The Lower Curves are for Coarse Sand Packed to a Porosity of about 34%. The Upper Curves are for Finer Sand or Looser Packings (Porosity > 34% ). Fine Sand 200-270 Mesh, Medium Sand 40-200 Mesh, Coarse Sand 20-30 Mesh (After Blackwell, 1962)

Some values for the parameters in eq. (5‑65) are as follows (Perkins and Johnston, 1963; Fried and Combarnous, 1971):

δ =	0.5	longitudinal dispersion
δ =	0.016	longitudinal dispersion
σ =	3.5	unconsolidated random bead pack
σ =	1.0	unconsolidated medium of identical spherical beads
σdp	0.25-0.46 cm	Berea sandstone
σdp	0.36 cm	average for some consolidated sandstones

 
In consolidated porous media, the particle diameter d_p loses it’s meaning, and σ and d_p are lumped together. It must be kept in mind that these parameters are strongly system dependent and cannot be universally applied (Brigham et al., 1961; Blackwell, 1962; Fried and Combarnous, 1971; Batycky et al., 1982). The majority of studies have been carried out with unconsolidated media, but some values for consolidated rocks are also available. Brigham et al. (1961) list parameters for glass bead packs of different bead diameters, Torpedo sandstone, and Berea sandstone. Spence and Watkins (1980) have determined σdp for a large number of Berea and Boise sandstone and San Andres carbonate cores.

Some of the factors that determine dispersion in porous media have been described by Perkins and Johnston (1963), and include particle size distribution, particle shape, packing or permeability heterogeneities, density and viscosity effects, turbulence, the presence of an immobile phase, capacitance, and wall effects. Patel and Greaves (1987) present experimental data to illustrate the effects of permeability, porous medium type (unconsolidated sand and consolidated sandstone), phase saturation, phase type, surfactant concentration, and interfacial tension.

As has been mentioned, the longitudinal dispersion coefficient is usually found to depend on velocity raised to a power between 1 and 1.25 at experimental conditions typical for laboratory core floods. This dependency has been found to hold for different types of porous media in single and two-phase flow. Some examples are bead packs (Brigham et al., 1961; de Smedt and Wierenga, 1979b), consolidated sandstone (Brigham et al., 1961; Baker, 1977; Ramirez et al., 1980; Spence and Watkins, 1980; Salter and Mohanty, 1982; Sorbie et al., 1985), consolidated sandstones with two-phase flow (Ramirez et al., 1980), and carbonate rocks, which usually have a more heterogeneous pore structure than sandstones and may exhibit dual porosity (Baker, 1977; Spence and Watkins, 1980).

Although the velocity dependence of the dispersion coefficient is similar in different porous media, the magnitude of dispersion is usually found to be higher in consolidated than in unconsolidated media (Brigham et al., 1961; Perkins and Johnston, 1963; Fried and Combarnous, 1971), and higher in carbonates than in sandstones (Baker, 1977; Batycky et al., 1980; Spence and Watkins, 1980; Bretz et al., 1986). It increases when the pore size distribution becomes wider (Spence and Watkins, 1980; Bretz et al., 1986) or the phase saturation decreases (Stalkup, 1970; Ramirez et al., 1980; Patel and Greaves, 1987; Sorbie et al., 1985), and is higher in the non-wetting than in the wetting phase (Patel and Greaves, 1987; Salter and Mohanty, 1982; Maini et al., 1986). The effect of phase saturation and wettability on dispersion can be attributed to the connectivity and tortuosity of the phase in question. The presence of a second, immiscible phase changes the flow geometry, and wettability determines liquid distributions. Dispersion increases when the viscosity ratio of displaced to displacing fluid increases towards unity. When the viscosity ratio exceeds unity, the one-dimensional convection-dispersion equation (Equation 7) no longer applies.