Fundamentals of Fluid Flow in Porous Media

 

Chapter 5

Miscible Displacement

The Equation of Continuity in Porous Media: Equation of Dispersion in Capillaries

Dispersion in cylindrical capillaries containing flowing fluids has been described mathematically in a paper by Taylor (1953). Consider a slug of tracer that is introduced into fully developed laminar flow. The velocity profile in a capillary of circular cross-section is parabolic. Since the velocity in the tube increases from zero at the walls to a maximum value at the center, the tracer would, in the absence of other effects, eventually disperse throughout the length of the tube. However, it is observed experimentally that a symmetrical mixing zone develops around a plane that travels at the mean speed of flow. This is not unlike the stationary case above, except that the mixing zone moves along the tube. The reason is molecular diffusion. Initially, the velocity profile distorts the tracer slug into parabolic shape. This sets up radial concentration gradients, which give rise to molecular diffusion in the radial direction. Given sufficient time, radial concentration gradients are eliminated by molecular diffusion. In the fully established mixing zone, the solute concentration is equalized radially, but depends on the axial distance from a plane that moves at the mean speed of flow, as illustrated in Figure 5‑53.

In its most general form, the tracer concentration in a capillary is given by the two-dimensional unsteady convective diffusion equation in cylindrical coordinates:

Where,

c = point concentration (a function of radial and axial position, and time),

u(r) = parabolic laminar velocity profile,

r = radial distance,

x = axial distance.

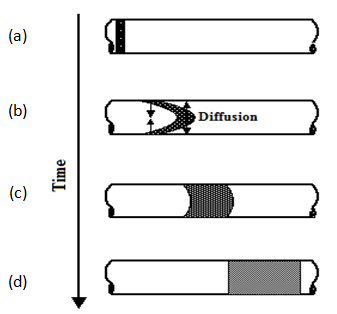
Figure 5-53: Development of the Mixing Zone as a Function of Time During Laminar Flow in a Capillary (After Nunge and Gill, 1970)

For “long” times, i.e. when the mixing zone in Figure 5‑53.d has been fully established, which is equivalent to saying that equalization of concentrations by molecular diffusion in the radial direction is fast compared to mixing by convection, Eq. (5‑60) can be shown to simplify into one-dimensional form (Taylor, 1953):

Where,

c_m = Tracer concentration at distance z and time t,

u_m = mean speed of flow,

K = hydrodynamic dispersion coefficient in the capillary.

Note that cm is no longer a function of radius, since concentrations are equalized radially. Also note that Eq. (5‑61) is of the same form as the one-dimensional equations of continuity discussed above (Eqs (5‑56) and (5‑59)), without the source/sink term. Thus, for “long” times, flow in the capillary can be described by the one-dimensional convection-dispersion equation.

The dispersion coefficient for porous media or capillaries is a parameter in Eqs (5‑58), (5‑59), and (5‑61). Hydrodynamic dispersion is the macroscopic outcome of the mixing of one fluid in a second, miscible fluid of different composition during flow through capillary spaces or porous media. The coefficient of hydrodynamic dispersion is a measure at which material will spread out in the system, hence of the length of the mixing zone. The mixing zone can be defined as that region of a capillary or porous medium where the concentration of an injected species changes from zero to the injected concentration, or from some imposed lower to an upper limit. The dispersion coefficient has the same units as the molecular diffusion coefficient (length squared per unit time).

For “long” times, it has been shown that the effective dispersion coefficient for flow in capillaries can be expressed as follows (Perkins and Johnston, 1963; Nunge and Gill, 1970; Fried and Combarnous, 1971; Bear, 1972):

Where,

K_L = effective dispersion coefficient for flow in capillaries,

∝ = constant that depends on capillary radius,

a = characteristic dimension of the capillary cross-section.

For a capillary of circular cross-section, a is radius, and ∝ = 1/48.

The right hand side of Eq. (5‑62) contains a diffusive and a convective term, and reflects the fact that dispersion in capillaries is the result of molecular diffusion and mechanical mixing due to flow. K_L represents axial (longitudinal) dispersion, since concentrations are equalized radially. The diffusion term, the first term on the right hand side, is a measure of dispersion by axial molecular diffusion, and the second term represents mixing due to flow and radial diffusion. At high velocities, the molecular diffusion term becomes negligible and dispersion is dominated by the convective term. At low velocities or high rates of diffusion, axial molecular diffusion contributes to dispersion. Molecular diffusion in the axial direction increases dispersion. Molecular diffusion in the radial direction decreases dispersion. Dispersion increases at higher velocities and with increasing tube radius.

“Long” time, as referred to above, refers to times long enough to eliminate radial concentration gradients by molecular diffusion. “Long” in this context is a relative term, depending on the relative rates of diffusion and convection. The minimum time required for the convection-dispersion model (or dispersion model, for short) to hold has been discussed in detail by Nunge and Gill (1970). It depends on a number of factors, such as capillary geometry, inlet boundary conditions, the type of concentration change (step change versus slug stimulus), laminar or turbulent flow, developing or fully developed flow fields, and fluid properties (density and viscosity differences). The minimum time is frequently expressed as dimensionless time (τ) and correlated with the Peclet number (Pe),

As an example, for fully developed laminar flow in capillary tubes with a step change in input concentration, the dispersion model holds for τ > 0.8. A summary of the regions of applicability of different models, taken from Dullien (1992) and Nunge and Gill (1970), is shown in Figure 5‑54. The Taylor-Aris theory in Figure 5‑54 is represented by Eq. (5‑62), while the Taylor theory is Eq. (5‑62) without the diffusion term (the first term on the right hand side). When τ < τ_min, the dispersion model (Eq. (5‑61)) does not apply and more complex models (Eq. (5‑60)) have to be used.

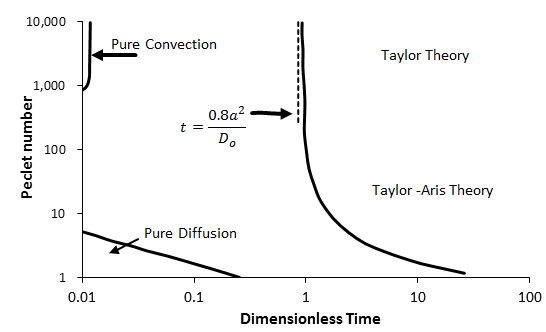
Figure 5-54: Summary of the Regions of Applicability of Various Analytical Solutions for Dispersion in Capillary Tubes with Step Change in Inlet Concentration as a Function of Dimensionless Time and Peclet Number (From Dullien, 1992)