Fundamentals of Fluid Flow in Porous Media

 

Chapter 3

Diffusion Coefficient: Effective Diffusion Coefficient

Experiments and field data show that the diffusion process in porous media is slower than that of two liquids adjacent to each other in a vial. This results from the fact that the diffusion coefficient in porous media is smaller than the bulk diffusion coefficient; therefore, an effective diffusion coefficient is proposed, which is based on the average cross-sectional area open to diffusion and the distance traveled by molecules in porous media.

For a bundle of straight capillary tubes, the effective diffusion coefficient and the bulk diffusion coefficient are the same. However, the straight capillary model is not a very good representation of a porous rock. A lot of work has been done to predict the apparent diffusion coefficient in porous media. Carman (1939) has shown that, in porous rock, fluids must move on the average at about 45° to the direction of flow (Figure 3‑5). Hence, when fluid has traveled a net distance, L, it has traveled an actual average distance of about √2 x L. On the other hand he assumed a tortuosity ( τ ) equal to √2 for the porous medium. Carman proposed the following ratio between the bulk and effective diffusion coefficients:

Where,

D_eff = Effective Diffusion Coefficient,

D = Molecular Bulk Diffusion Coefficient.

Here 0.707 is a correction for the actual diffusion process length.

On the other hand in the porous medium the cross section area available for diffusion is not the total cross section of the medium. By assumption of the equality between areal and volume porosity it can be concluded that only a portion (equal to the porosity) of the total cross section of the medium is available for diffusion process. According to this assumption Penman (1940), after some experiments on a packing of spherical particles, proposed the next equation to relate the bulk and effective diffusion coefficient to each other:

Where, φ is the porosity. In this formula, 0.66 is the correction for real length of diffusion process and φ is the correction for actual area available for diffusion.

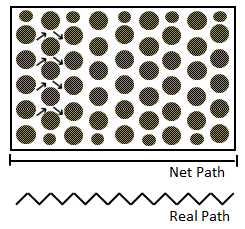
Figure 3-5: In a Porous Medium Fluid Generally Flowing at about 45° with respect to Average Direction of Flow

On the other hand grain shapes and sizes of a porous medium are not homogeneous all the time so the assumption of constant values such as 0.707 or 0.66 is not reasonable to use as the inverse of the tortuosity, so it could be more sophisticated to use the tortuosity in the formula instead of a constant value:

A more sophisticated and comprehensive approach was suggested by Brigham, Reed et al. (1961) and van der Poel (1962). These investigators recognized that there is an analogy between diffusion and the electrical resistivity factor with the following formula:

Where, F is the formation resistivity factor. Diffusion coefficient in the absence of the porous media, is sometimes called bulk diffusion coefficient in contrast to the effective diffusion coefficient at the presence of the porous medium.