Fundamentals of Fluid Flow in Porous Media
Chapter 3
Diffusion Coefficient: As a Function of Concentration
The diffusion coefficient can be considered constant in many occasions especially when we refer to the diffusion of gases Dimensions and shape: The molecular diameter and molecular shape should be similar for the diffusing components. That means in this case that the molecular diameter and shape of the solvent should be similar to those of the heavy oil and bitumen. We know that large hydrocarbon chains are present in heavy oil and bitumen. Thus the assumption of similar size and shape is not valid especially when we take into consideration that the solvents used in the recovery process are light gases and small hydrocarbons molecules. Molecular interactions: The molecular interactions between the diffusing components should be negligible. That means the attraction and repulsion forces should not interfere in the diffusion process. However, it has been shown that the repulsive forces play the most important role in the diffusion process. Non reacting environment: There should be a non-reacting environment in the system. That means no transformations of any kind due to the components on the system and/or the system conditions (pressure and temperature). However the interaction of solvent with heavy oil or bitumen may in some cases cause organic deposition, mainly asphaltenes. Based on the concentration dependency of the diffusion coefficient Fick’s second law is modified as follows: Example 3-2 Proof eq. (3‑22) Solution Assume a control volume like as Figure 3‑4. There is no source or sink in the control volume. Solvent diffuses in from left hand side and go out by diffusion from right hand side. Write material balance for solvent in over the control volume: Where: V = Volume, A = Area available for diffusion, C = Solvent concentration, D = Diffusion coefficient, Δt = incremental time. According to the dependency of diffusion coefficient on the concentration Dx ≠ Dx + Δx, because we have a diffusion process and the potential for this process is concentration difference between x and x + Δx. With a constant area: V = A x Δx. Now divide both side of eq.(3‑23) by V x Δt: [1] “The Diffusion Coefficient of Liquid and Gaseous Solvents in Heavy Oil and Bitumen”, U.E. Guerrero-Aconcha If you have any questions at all, please feel free to ask PERM! We are here to help the community.

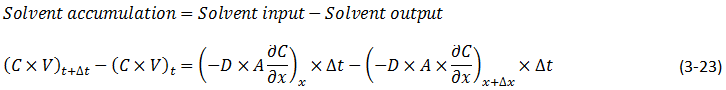
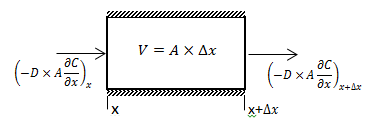
Figure 3-4: Diffusion Process in a Control Volume with a Concentration Dependent Diffusion Coefficient
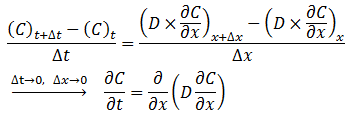
References
Questions?
