Fundamentals of Fluid Flow in Porous Media
Chapter 2
Porosity:
Laboratory Porosity Measurement
A great many methods have been developed for determining porosity, mainly of consolidated rocks having intergranular porosity (encountered in oil reservoir). Most of the methods developed have been designed for small samples. From the definition of porosity it is obvious that common to all methods is the need to determine two of three volumes: total or bulk volume of the sample, its pore volume, and/or the volume of its solid matrix. The various methods based on such volume determination, called “direct methods”, differ from each other in the way these volumes are determined. Other methods are available, called “indirect methods” based on the measurement of some properties of the void space. Examples of such properties are the electrical conductivity of electrically conducting fluid filling the void space of the sample, or the absorption of radioactive particles by a fluid filling the void space of the sample. The porosity of the larger portion of rock is determined statistically from the results obtained on numerous small samples.
Bulk volume
The simplest direct method for determining bulk volume of a consolidated sample with a well design geometric shape is to measure its dimensions. The method is applicable to cylindrical core with smoothed flat surfaces. The usual procedure is to determine the volume of fluid displaced by the sample. This method is particularly desirable for irregular shaped samples. The fluid volume that the sample displaces can be determined volumetrically or gravimetrically. In both methods the displaced fluid should be prevented from penetrating the pore space of the sample. There are 3 strategies to do that:
- Coating the rock sample with paraffin
- By saturating the rock with the fluid into which it is to be immersed
- By using mercury, which according to its surface tension and wettability characteristics does not tend to enter to small pores of most intergranular samples?
Gravimetric determination of the bulk volume can be accomplished by measuring the loss in the weight of sample when it is immersed in the fluid or observing the change in the weight of pycnometer when is filled with mercury and when is filled with mercury and core sample.
Example 2‑2
Bulk Volume Calculation of coated sample immersed in water.
A = weight of dry sample in air = 30.0 g
B = weight of the sample after coating with paraffin = 31.8 g; Paraffin density = 0.9 g/cm3
C = weight of paraffin = B – A = 1.8 g
D = volume of paraffin = 1.8 / 0.9 = 2cm3
E = weight after immersing of the coated sample in the water = 20 g, water density = 1 g/cm3
Volume of water displaced = (B – E) / water density = 11.8 cm3
Bulk volume of rock = volume of water displaced – volume of paraffin = 9.8 cm3
Example 2-3
Calculate the volume of a dry sample immersed in mercury pycnometer.
A = weight of dry sample in air = 30 g
B = weight of pycnometer filled with mercury at 20oC = 360 g, mercury density = 13.546 g/cm3
C = weight of pycnometer filled with mercury and sample at 20oC = 245.9 g
D = weight of sample + weight of mercury filled pycnometer = A + B = 390 g
E = Weight of mercury displaced = D – C = 144.1 g
Bulk volume of rock = E/mercury density = 144.1 / 13.546 = 10.6 cm3.
Grain volume
The grain volume can be determined from the dry sample weight and the grain density. For many purposes, result with sufficient accuracy can be obtained by using the density of quartz (2.65 g/cm3) as the grain density.
A method of determining the gain volume is crushing the sample after determining the bulk volume, thus removing all pores including the non-interconnecting ones. The volume of solids is then determined by fluid displacement in a pycnometer.
Pore volume
There are methods to measure the pore volume of the rock sample directly with no need to determine the grain volume. Actually, all these methods measure effective porosity. The methods are based on the extraction of a fluid from the sample or intrusion of a fluid into the pore space of the rock sample.
Mercury injection method:
Both the bulk and pore volume are determined in this method. The tested sample is placed in a chamber filled to a certain level with mercury, with a known volume of air at a known pressure (e.g. atmospheric pressure) above it. The volume of mercury displaced by the sample gives the bulk volume. When the pressure of mercury is increased by a volumetric pump, the mercury penetrates the pore space of the sample. Total effective pore volume could be determined by gradually increasing the pressure. In general the method is not suitable for low permeability samples as very high pressure are required.
Gas expansion method:
This method is based on the Boyle-Marriote Gas Law. It may be the most widely used method for determine porosity. The test usually carried out at the constant temperature. Basically two chambers with known volumes are connected by a valve (Figure 2‑10). The tested sample is placed in the chamber of volume V1. The pressure in this chamber is P1. The second chamber (volume V2), initially at pressure P0, is connected to the first one by opening the valve between them, thus permitting the gas to expand isothermally. If the final pressure is P2, from Boyle-Marriote law we have:

Where Vs = grain volume.
Usually, for simplification, helium as an approximately ideal gas, at low pressure, is used and according the ideal gas assumption Z=1;
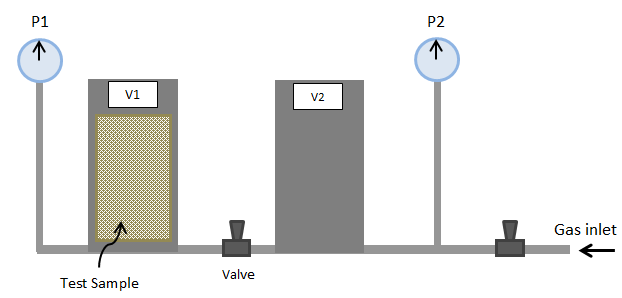
Figure 2-10: Porosimeter Based on Boyle – Mariotte’s Law
Imbibition method:
Reservoir rocks have the ability of imbibe water spontaneously. This property is used to determine effective porosity of the rock. In this method the weight of a dry sample is measured and then the sample is immersed under vacuum in water or any other fluid that rock has the tendency to imbibe. After enough time, up to several days, the saturated sample is weighted. Utilizing the density of the liquid we can find the imbibed fluid volume and subsequently the effective porosity of the sample.
Optical methods:
The porosity of a sample is equal to the “areal porosity” provided that pore structure is random. The areal porosity is determined on polished thin sections of a sample. It is often necessary to impregnate the pore with some material such as wax, plastic, color, or wood’s metal in order to make pores more visible and/or distinguishing interconnected pore from the isolated pores (Figure 1‑1). When impregnating the sample with a resin only the interconnected pores will be invaded. Whenever there are very small pores present along with large ones, it is very difficult to make sure that all the small pores have been accounted for by the measurement. This is one of the reasons why the porosity measurements by the optical methods may differ significantly from the results obtained by other methods.

Figure 2-11: Colored Thin Section Microscopic Image
Statistical methods:
A pin is dropped many times in a random manner on an enlarged photomicrograph of a section of consolidated porous material, the porosity of which is to be determined. It can be shown that the probability of a random point falling within the pore space of this section is equal to the porosity. Therefore, as the number of tosses increases, the number of times the pin’s point falls in the pore space to the total number of tosses approaches the value of the porosity.
X-ray tomography methods:
ADD TEXT TO SECTION (Section Not Complete)
Magnetic resonance methods:
ADD TEXT TO SECTION (Section Not Complete)
