Fundamentals of Fluid Flow in Porous Media

Chapter 2

Multi-phase Saturated Rock Properties:

Phase Trapping: Bypassing

According to the Pc equation, at the same condition non-wetting phase tends to invade the larger pores because of the lower capillary pressure. This tendency leads to special trapping mechanism named bypassing. The main trapping mechanism in drainage is bypassing although during the imbibition process non-wetting phase could be trapped by bypassing mechanism but it is not the major trapping mechanism.

A reservoir rock consists of a complex network of branching and reuniting pore elements of differing sizes and geometry. Any successful analysis of the displacement process should eventually recognize this complex network. However one can begin by understanding the processes which take place in the simpler elements of the network. The mechanisms of drainage displacement and imbibition displacement are best illustrated by visualization of flow experiments in transparent capillary networks etched on glass plates. The simplest type of pore system used in such displacement studies is the pore doublet (Figure 2‑69).

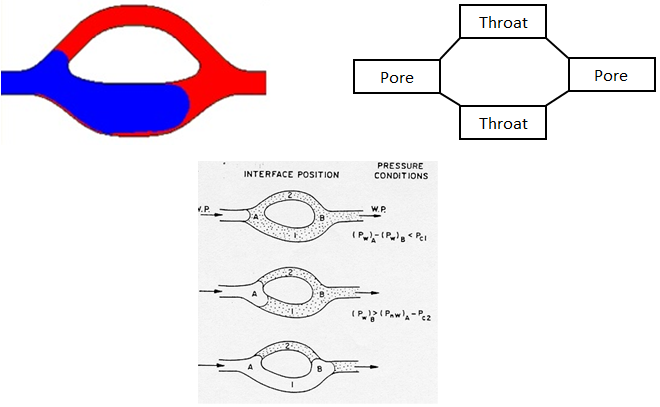
Figure 2-69: Pore Doublet Model

Smaller throat is invaded first during the imbibition because of higher capillary pressure and larger throat is swept first during the drainage process.
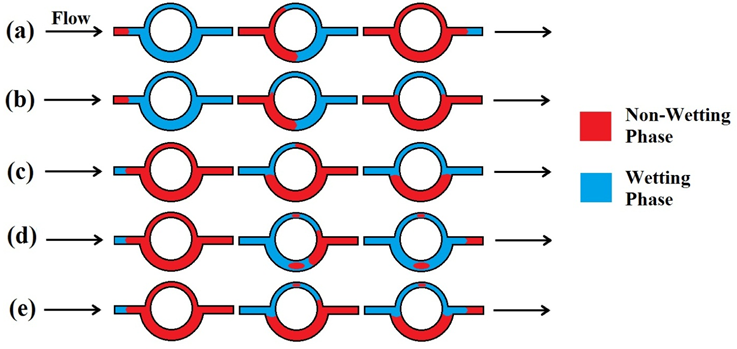
Drainage and Imbibition Processes in pore doublet model
(a) Drainage Process, No Trapping
(b) Drainage Process, Bypassing in Smaller Throat
(c) Imbibition Process, Bypassing in Larger Throat
(d) Imbibition Process, Snap-Off
(e) Imbibition Process, Snap-Off in Smaller Throat and Bypassing in Larger Throat

Figure 2‑70 illustrates the drainage and imbibition mechanisms for the pore doublet model.

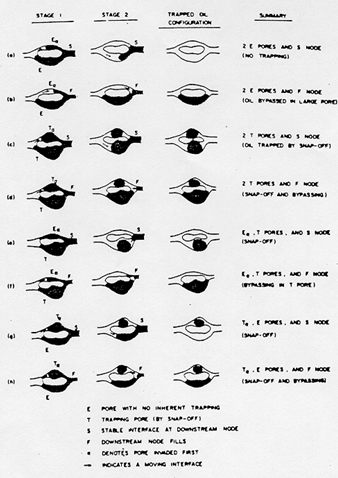
Figure 2-70: Imbibition and Drainage Mechanisms in a Pore Doublet Model

The condition that bypassing happen in the larger pore during the imbibition could be found by using the capillary and viscous forces formula.

Assume a pore doublet model as in Figure 2‑71.

For pore #1:
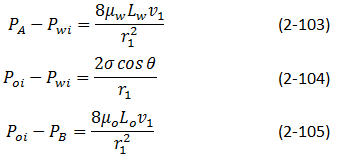
Capillary and Viscous Forces Formula (Equation 2-103, 2-104, 2-105)

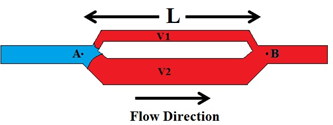
Figure 2-71: Pore Doublet Model for Illustration of Displacement and Trapping of Oil[1]

Assume μ_w = μ_o = μ and defining L = L_o + L_w, we get
Equation 2-106

Similarly for second pore:
Equation 2-107

The overall pressure change is same for both pores, therefore:
Equation 2-108

This equation gives a relationship between v1 and v2:
Equation 2-109

For v2 to be positive (no trapping by bypassing), we must satisfy
Equation 2-110

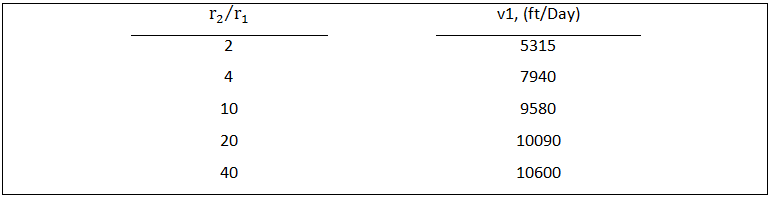
The values of v1 needed to make v2 positive are listed in Table 5 for a typical case. At reservoir type velocities, v2 will not be positive and oil will be displaced only from the smaller pore. Once the water breaks through at the other end of the pore doublet, the oil in the larger pore is trapped and very difficult to mobilize.

Table 5: Pore Doublet Model, Required Velocity in Small Pore to Maintain Zero Velocity in Large Pore (r1=2.5μm)