Fundamentals of Fluid Flow in Porous Media

 

Chapter 2

Formation Resistivity Factor:

Effect of Conductive Solids

The clay minerals present in natural rock act as a conductor and are sometimes referred to as “conductive solids”, but it is actually the water in the clay and the ions in the water that are the conducting materials.  Figure 2‑31 shows variation of formation factor with water resistivity for clean and clayey sands.  The effect of the clay on the resistivity of the rock is dependent upon the amount, type and manner of distribution of the clay in the rock.

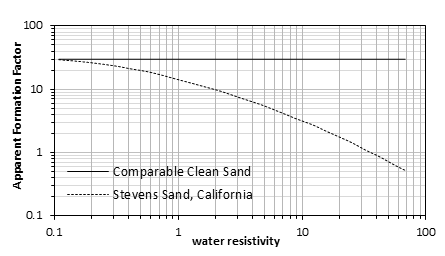
Figure 2-31: Apparent Formation Factor vs. Water Resistivity for Clay and Clean Sands

As shown in Figure 2‑31 the formation factor for a clay-free sand is constant.  However, the formation factor for a clayey sand increases with decreasing water resistivity and approaches a constant value at a water resistivity of about 0.1 Ω·m.  The apparent formation factor F_a was calculated from the definition of the formation factor and observed values of R_oa and R_w (F_a = R_oa/R_w).  Wyllie proposed that the observed effect of clay minerals was similar to having two electrical circuits in parallel: the conducting clay minerals and the water-filled pores.  Thus,

Where R_oa is the resistivity of shaly sand when 100% saturated with water of resistivity R_w.  R_c is the resistivity due to the clay minerals.  FR_w is the resistivity due to the distributed water, and F is the true formation factor of the rock (the constant value when the rock contains low-resistivity water).

Rearrange equation (2‑51)

From equation (2‑52)

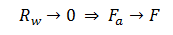
Therefore, F_a approaches F as a limit as R_w becomes small.  This was observed in Figure 2‑31.

The data presented in Figure 2‑32 shows the relationship expressed in the previous equation.  The plots are linear and are of the general form:

Where C is the slope of the line and b is the y-intercept.  Comparing with the equation (2‑51), it may be noted that C = 1/F and b = 1/R_c.  The line in which b = 0 indicates a clean sand.

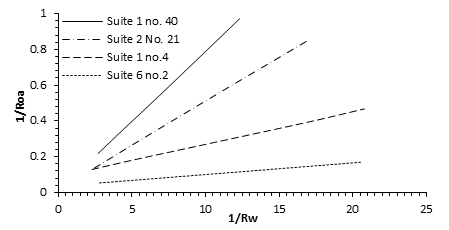
Figure 2-32: Water-Saturated Rock Conductivity as a Function of Water Conductivity